Чувствительность систем управления к изменению параметров

Объект управления, представленный передаточной функцией W₁(p), какова бы ни была его природа, подвержен влиянию окружающей среды, старению, отсутствию точной информации об его параметрах и других объективных факторов, которые негативно сказываются на его поведении. В разомкнутой системе с ПФ W(p)= W₁(p)W₂(p) все эти факторы приводят к отклонению выходной переменной (управляемой величины) от желаемого значения. Замкнутая система, напротив, чувствует это отклонение, обусловленное изменениями параметров объекта, и пытается скорректировать выходную переменную. Поэтому чувствительность системы управления к изменению параметров есть вопрос первостепенной важности. Основное преимущество систем с обратной связью состоит в их способности снижать чувствительность к изменению параметров.

В случае замкнутой системы, если для всех представляющих интерес значений частоты W(p)>>1, 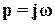, то из

Ф(р)=W(p)/|1+W(p)| (1)

мы имеем

y(p)≈v(p).

Следовательно, мы в точности достигаем желаемого результата, т.е. выход становится равным входу. Однако прежде чем использовать эту идею для построения системы управления, мы должны заметить, что условие | W(p)|>>1, 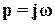, может привести к тому, что реакция системы будет сильно колебательной или даже к потере системой устойчивости. Но, тем не менее, тот факт, что, увеличивая модуль функции |W( 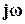)|, мы уменьшаем влияние изменений в W(p) на выходную переменную, является исключительно ценным. Таким образом, важным преимуществом системы с обратной связью является то, что в ней уменьшается влияние изменений параметров объекта управления.

Чтобы проиллюстрировать сказанное выше, рассмотрим случай, когда за счет изменений параметров объекта его передаточная функция приняла выражение 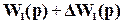. Тогда, если система является разомкнутой, выходная переменная (управляемая величина) (в виде изображения по Лапласу) получит приращение

,

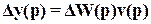где 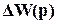= 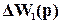W₂(p) – изменение ПФ разомкнутой системы.

В замкнутой системе мы имеем

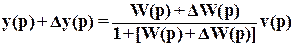. (1а)

Отсюда приращение выходной переменной:

.

Если 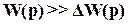, как это часто имеет место, то

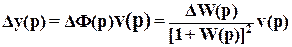, (2)

где 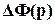- изменение ПФ замкнутой системы.

Анализ выражения (2) показывает, что в замкнутой системе изменение выходной переменной уменьшается в [1+W(p)]² раз; в свою очередь член [1+W(p)] обычно много больше единицы в представляющем интерес диапазоне комплексной частоты. Сомножитель 1+W(p) играет очень важную роль в определении характеристик систем с обратной связью.

Чувствительность системы определяется как отношение процентного изменения передаточной функции системы к процентному изменению передаточной функции объекта. Система имеет передаточную функцию

Ф(р)=y(р)/v(p),

и, следовательно, чувствительность определяется, как

. (3)

В пределе, переходя к малым изменениям, (3) приводится к виду:

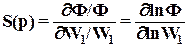. (4)

Чувствительность системы – это отношение изменения ее передаточной функции к изменениям передаточной функции (или параметров) объекта управления при условии их малости.

Из (1а) следует, что чувствительность разомкнутой системы равна единице. Чувствительность замкнутой системы легко можно получить из (4). Замкнутая система имеет передаточную функцию

.

Следовательно, ее чувствительность c учетом (2)равна

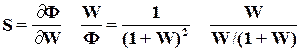
или

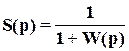. (5)

Отсюда еще раз видно, что чувствительность замкнутой системы можно сделать меньше, чем ее чувствительность в разомкнутом состоянии, путем увеличения Ф(р)=W( 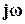) в представляющем интерес диапазоне частот. Заметим, что чувствительность системы при малых изменениях параметров и (или) передаточной функции определяется функцией чувствительности.

Заметим, что Ф(W)=W/(1+W) является нелинейной функцией. Отсюда найденная чувствительность говорит лишь о реакции системы на малые возмущения (изменения) относительно W(p). При больших возмущениях система может иметь радикально отличное поведение и даже может стать неустойчивой.

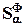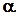Часто бывает необходимо определить чувствительность , где - параметр передаточной функции W(p). Используя правило дифференцирования сложной функции, можно записать:

.

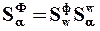Встречаются также случаи, когда передаточная функция системы Ф(р) имеет вид дроби:

,

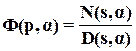где 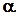- параметр, подверженный изменениям за счет внешних факторов. Тогда чувствительность системы к изменению 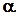можно записать, используя выражение (4):

,

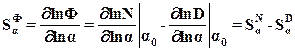где 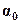- номинальное значение параметра.

Способность уменьшать влияние изменения параметра путем введения обратной связи – одно из положительных качеств замкнутых систем управления. Ч тобы добиться высокой точности управления в разомкнутых системах, необходимо очень тщательно подходить к выбору элементов, образующих передаточную функцию W(p). Напротив, замкнутые системы допускают определенные вариации параметров W(p), поскольку их влияние ослабляется в (1+W(p)) раз.

Дата добавления: 2014-01-07