Робастное качество

П, то желательно выбрать регулятор (УУ) с ПФ такой, который, как минимум, гарантировал устойчивость замкнутой системе для всех возможных реализаций объектов, взятых (принадлежащих) из множества П. Это свойство замкнутой системы оставаться устойчивой для всех возможных реализаций известно как робастная устойчивость.

Робастная устойчивость

Лекция 33

В предыдущем параграфе мы рассмотрели метод оценки неопределенности в моделях динамики ОУ. Если данный ОУ принадлежит к множеству моделей

Не в пример ОУ мы можем предположить, что мы знаем ПФ регулятора 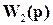точно. Тогда ПФ возмущенной разомкнутой системы будет являться элементом множества

Л: =,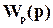

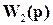
где W_1р(p) П. Для дальнейшего анализа предположим, что П естьмножество ОУ с ПФ

,

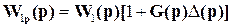т.е. представляет собой мультипликативную неопределенность. Аналогично можно трактовать множество ПФ разомкнутых систем

Л: 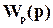=, (6)

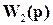
где =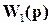есть ПФ номинальной разомкнутой системы.

Мультипликативное представление неопределенности является предпочтительным в сравнении с аддитивной представлением. Дело в том, что при первом представлении границы неопределенности остаются неизменными как для объекта, так и для разомкнутой системы. Также с помощью мультипликативного представления неопределенности проще формулировать условия робастной устойчивости и качества.

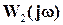
Вспомним, что в соответствии с критерием Найквиста: если разомкнутая (номинальная) система устойчивая, то для устойчивости замкнутой (номинальной) системы необходимо и достаточно, чтобы АФХ разомкнутой (номинальной) =системы не охватывала т. (-1,j0) (рис. 7).

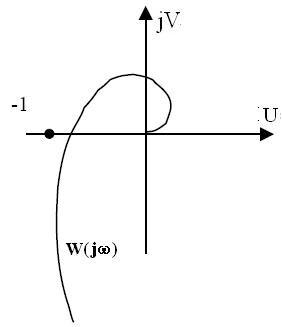
Рис. 7

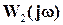
Робастная устойчивость требует, чтобы АФХ разомкнутой возмущенной (реальной) системы=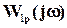не охватывала т. (-1,j0) для всех W_1р (p) П (рис. 8).

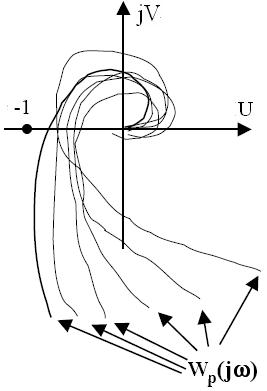
Рис. 8

Каким образом можно это гарантировать? Для мультипликативной неопределенности АФХ реальной системы описывается выражением

=, (7)

которое представляет собой векторное уравнение. Это векторное уравнение можно отобразить на комплексной плоскости (рис. 9).

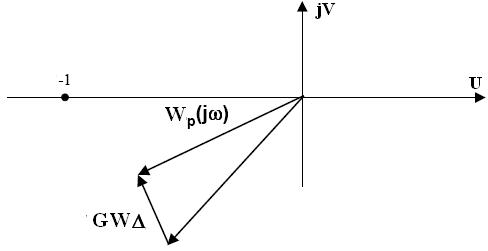
Рис. 9

.

Так как вектор в (7)

=

может иметь любую фазу и 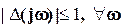, то вектор 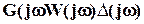при , определяет окружность с центром в точке и радиусом 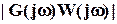. Внутри этой окружности для данного 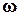располагаются концы векторов при , другими словами, значения АФХ всех систем, входящих в множество Л. При этом верхнее граничное (максимальное) значение АФХ 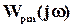для конкретного значения 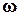представляет собой вектор, проведенный из начала координат в произвольную точку, расположенную на этой окружности (рис. 10).

Рис. 10

Т. к. робастная устойчивость гарантирована, если АФХ реальной системы не охватывает точку(-1,j0) для всех частот 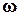, то нетрудно видеть, что для этого необходимо, чтобы вышеописанная окружность с радиусом 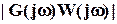не охватывала ту же точку.

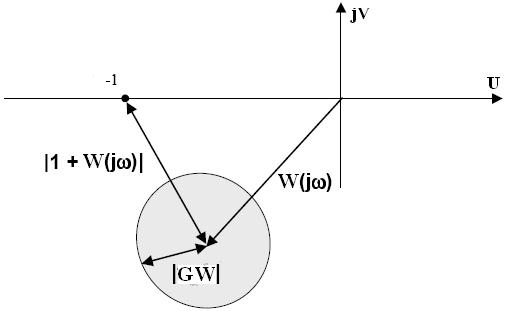
Рис.11

Из рис. 11 следует, что окружность с радиусом 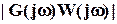с центром в т. не охватывает т. (-1,j0) для всех 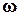, если

1) АФХ номинальной разомкнутой системы не охватывает т. (-1,j0) и

2) если выполняется условие

,

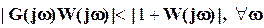называемое критерием робастной устойчивости.

Последнее условие эквивалентно условию

.

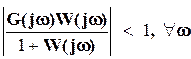Т.к. дополнительная функция чувствительности T=W/(1+W), критерий робастной устойчивости можно записать как

(8)

или как

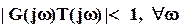. (9)

Используя норму для краткости, можно критерий робастной устойчивости представить в виде

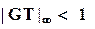. (10)

Применение нормы имеет своей целью получить консервативное условие устойчивости, т.е. для возможной наихудшей реализации анализируемой модели ОУ.

Из уравнения (8) следует, что АЧХ номинальной замкнутой системы |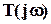)| должна на всех частотах проходить ниже обратной АЧХ границы неопределенности 1/. Рассмотрим типичный случай объекта с плохо известной высокочастотной динамикой (рис. 12), так что

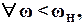
- <<1

- >> 1 .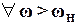

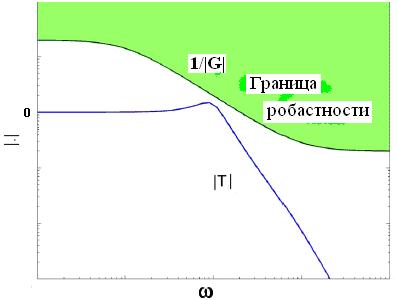
Рис. 12

Вывод. При высокочастотной неопределенности мы должны ограничивать полосу пропускания номинальной замкнутой системы, если мы хотим добиться робастной устойчивости.

Правило. Прежде чем проверять выполняются ли условия робастной устойчивости надо оценить, устойчива ли номинальная замкнутая система.

Алгоритм анализа робастной устойчивости:

1. Найдите ПФ регулятора W₂ (p), используя номинальную ПФ объекта

W₁ (p),

2. Постройте границу для модели неопределенности G(p) ( устойчивая, минимально-фазовая).

3. Проверьте, выполняется ли условие .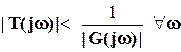

Алгоритм синтеза робастной устойчивости:

- непосредственно путем метода проб и ошибок проектируется регулятор, чтобы обеспечить выполнение условия .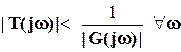

- Более трудный путь использовать технологию синтеза.

Номинальное качество. Мы показали в лекции 31, что основные требования к качеству замкнутой системы, в рассматриваемом случае к номинальной замкнутой системе, можно записать в виде одного требования

,

касающегося взвешенной функции чувствительности. Здесь 1/|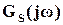| представляет собой допустимую верхнюю границу функции чувствительности | S(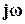)|, соответствующую устойчивой минимально-фазовой ПФ G_S (p), которая выбирается обычно в виде

,

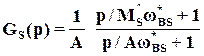причем 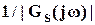равна A (типично малая величина 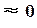) на низких частотах и равна 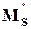> 1 на высоких частотах.

Чтобы наглядно представать это требование, запишем его в другом виде

или, что - то же самое

.

Вспомним, что 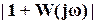есть расстояние от критической точки (-1,j0) до каждой точки, расположенной на АФХ разомкнутой номинальной системы (рис. 13. Условие номинального качества требует, чтобы это расстояние было больше, чем радиус . Для проверки этого условия надо построить окружность с радиусом и центром в точке (-1,j0), и оценить находится

Рис.13

ли АФХ разомкнутой системы целиком вне пределов этой окружности, причем это надо проделать для всех частот от 0 до (рис. 13).

Вывод. Критерий номинального качества: АФХ разомкнутой номинальной системы должна располагаться целиком вне окружности радиусом и с центром в точке (-1,j0) для всех частот.

Робастное качество. Для номинального качества требуется, чтобы

. (11)

Но для робастного качества мы требуем, чтобы для всех возможных моделей, принадлежащих множеству моделей П.

Для дальнейшего анализа предположим, что П естьмножество ОУ с ПФ 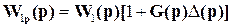, т.е. представляет собой мультипликативную неопределенность. Аналогично можно трактовать множество ПФ возможных разомкнутых систем

Л: =,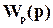

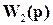
где =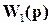есть ПФ номинальной разомкнутой системы.

Тогда можно определить

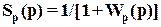
как множество возможных функций чувствительности для мультипликативной неопределенности.

Для выполнения условий робастного качества требуется, чтобы

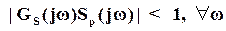(12)

для всех возможных реализаций 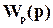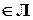. С учетом выражения для S_p (p) этот критерий робастного качества можно записать в другом виде

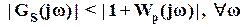(13)

для всех возможных реализаций .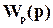

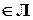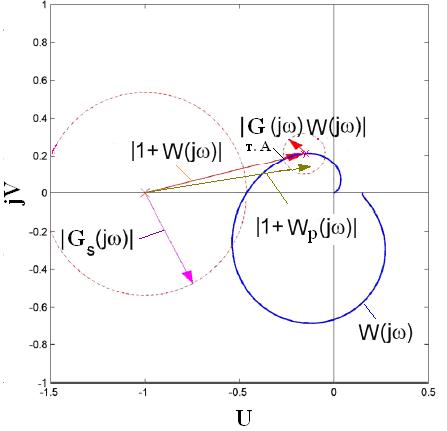
Рис. 14

Для конкретного значения частоты нужно, чтобы условие (13) выполнялось для модели ОУ, при которой длина вектора 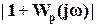является наименьшей. Как видно на рис. 14, длина вектора 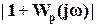будет

наименьшей 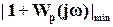в точке A пересечения вектора 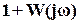с окружностью радиусом 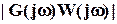с центром в т. . Отсюда наименьшая длина вектора равна разности длин векторов 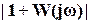и ,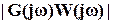

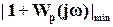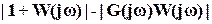=. (13а)

Следовательно, критерий робастного качества можно записать как

,

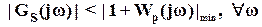или с учетом (13а)

.

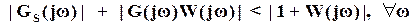Разделив левую и правую части последнего выражения на 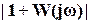, получаем

.

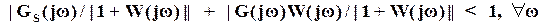Т.к. S=1/(1+W) и дополнительная функция чувствительности номинальной системы T=W/(1+W), то критерий робастного качества можно записать так

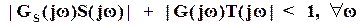, (14)

или с помощью бесконечной нормы

.

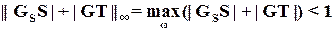Таким образом, критерий робастного качества является комбинацией критерия робастной устойчивости и критерия номинального качества. Ясно, что для обеспечения робастного качества мы, прежде всего, должны гарантировать номинальное качество (10) и робастную устойчивость (9) .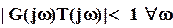

Дата добавления: 2014-01-07