Опустить. Графическая интерпретация критерия робастного качества такова (рис

Графическая интерпретация критерия робастного качества такова (рис. 14).

Для выполнения условия (13) требуется, чтобы все возможные значения АФХ разомкнутой возмущенной системы располагались целиком вне окружности радиусом с центром в т. (-1,j0). Но мы уже знаем из описания неопределенности, что все значения находятся внутри окружности радиусом 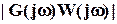с центром в т. для каждого значения частоты . Итак, для каждой частоты мы имеем две окружности: одну с центром в т. (-1,j0), связанную с требованиями качества, и другую с центром в т. , связанную с моделью неопределенности (рис. 14).

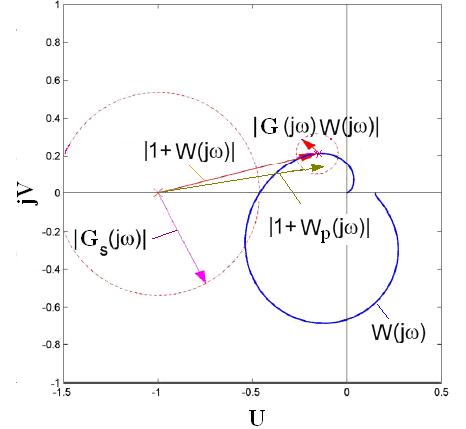
Рис. 14

Таким образом, критерий робастного качества (13)соблюдается для конкретного значения , если обе эти окружности не соприкасаются между собой.

Практически размеры (радиусы) этих окружностей зависят от частоты (рис. 15).

Рис. 15

Графическая проверка является несколько сложной. Найдем алгебраический метод анализа робастной устойчивости. Прежде всего, отметим, что расстояние между центрами окружностей (рис. 14) определяется как 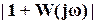. Следовательно, условие, при котором эти окружности не пересекаются, сводится к тому, чтобы их центры располагались на большем расстоянии друг от друга, чем сумма их двух радиусов, т.е., чтобы

.

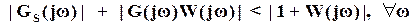или, чтобы

.

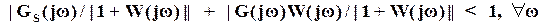Т.к. S=1/(1+W) и дополнительная функция чувствительности номинальной системы T=W/(1+W), то критерий робастного качества можно записать так

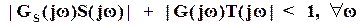(14)

или с помощью бесконечной нормы

.

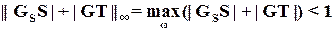Таким образом, критерий робастного качества является комбинацией критерия робастной устойчивости и критерия номинального качества. Ясно, что для обеспечения робастного качества мы, прежде всего, должны гарантировать номинальное качество (10) и робастную устойчивость (9) .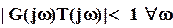

Дата добавления: 2014-01-07