Кислотно-основное титрование

Решение вопроса о соответствии характерной точки на кривой потенциометрического титрования, принимаемой за КТТ (точка перегиба на интегральной кривой или точка максимума на дифференциальной кривой), моменту эквивалентности всегда необходимо проводится на основе анализа уравнения кривой титрования. Вывод такого уравнения и его вид зависят от типа изучаемой реакции. Рассмотрим подробно такую задачу на примере протолитических реакций.

Кривые ПТ титрова­ния E = f(y ) (где y - концентрация добавленного титранта)являются отображением изменения в ходе титрования рН раствора. Поэтому в качестве ИЭ может быть выбран любой из перечисленных выше рН-чувствительныхэлектродов, потенциал которого зависит от концентрации ионов водорода.Чаще всего используют стеклянный электрод.

Для упрощения расчета КТ обычно оперируют концентрациями, а не активностями ионов, т.е. допускают, что растворы разбавлены и коэффициенты активности компонентов можно принять равными 1, или в растворе присутствует индеферентный электролит, который обеспечивает постоянство коэффициентов активности в ходе титрования. В этом случае можно оперировать величиной pH= −lg[H⁺], уравнение потенциала индикаторного электрода можно записать в виде:

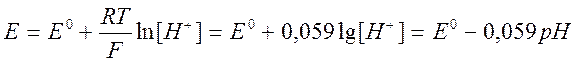(2.1)

Для всех водородных электродов эти уравнения будут отличаться только величиной E^o, поэтому полученные с помощью разных электродов кривые потенциометрического титрования будут идти симбатно.

При расчетах обычно пренебрегают разбавлением раствора в ходе титрования. При этих допущениях экспериментальные кривые не совпадают с теоретически рассчитанными кривыми. Однако возникающая при этом небольшая погрешность не имеет существенного значе­ния при определении рН конечной точки титрования.

Форма кривой и положение точки эквивалентности зависят от силы кислоты или основания. Для любой точки потенциометрической кривой потенциал электрода можно рассчитать по формулам для вычисления рН растворов соответствующих кислот и основа­ний. В случае кислот (оснований), которые полностью диссоци­ируют в растворе, необходимые данные можно получить сравни­тельно просто.Например, при титровании сильной кислоты силь­ным основанием, которое протекает согласно схеме

HA + BOH ® BA + H₂O (2.2)

КТpH=f(y ) легко получить на основании принципа электронейтральности растворов

[H⁺] + [B⁺] = [A-] + [OH-] (2.3)

Учитывая выражение ионного произведения воды K_w=[H⁺][OH^-] и численное равенство концентраций введенного основания и катионов металла при титровании кислоты, запишем

y = [B⁺] = [A^-] − [H⁺] + K_w / [H⁺] (2.4)

В ходе титрования сильной кислоты сильным основанием концентрация анионов будет оставаться постоянной (если пренебречь разбавлением раствора) и равной исходной концентрации кислоты C_o. Решив квадратное уравнение

y = C_o − [H⁺] + K_w / [H⁺]

[H⁺] – (C – y) – K_w = 0 (2.5)

получим выражение для расчета концентрации ионов водорода в ходе титрования

(2.6)

По найденным значениям [H⁺] можно рассчитать величины pH и потенциал индикаторного электрода E при заданных значениях y, т.е. рассчитать кривую титрования.

Для момента эквивалентности, когда y=C₀

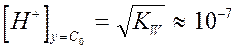, а pH_y=Co = 7 (2.7)

Чтобы оценить форму кривой нейтрализации и выбрать на ней характерную точку, отвечающую конечной точке титрования, необходимо проанализировать уравнение (2.5) т.е. найти выражения

первой производной dpH/dy (“податливость” системы),

второй производной d²pH/dy² и условия их равенства нулю.

На практике чаще пользуются величиной обратной “податливости”, которую называют “буферной емкостью” (или для краткости “буферностью”)

Р = dy/dpH = d[B⁺]/dpH (2.8)

Дифференциировать уравнение (2.5) по pH для нахождения буферности нельзя. Учитывая, что

dpH = d(-lg[H⁺]) = -0,43(dln[H⁺]) = - d[H⁺] / 2,3[H⁺] (2.9)

выражение для “буферности” можно получить, умножая уравнение (2.5) на −2,3[H⁺] и дифференциируя по [H⁺]:

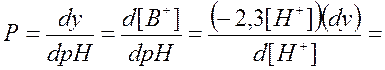
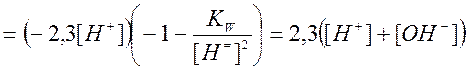(2.9)

Из последнего соотношения следует, что при любом значении pH растворов сильных протолитов P ≠ 0, поэтому кривая нейтрализации не имеет экстремума.

Чтобы выяснить имеет ли кривая титрования точку перегиба, необходимо выяснить как ведет себя буферность с изменением pH, т.е. найти выражение производной dP / dpH. Дифференциируя уравнение (2.10) с учетом (2.9), получим

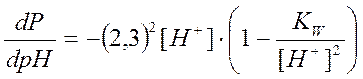(2.11)

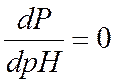, если (1- K_w/[H⁺]²)=0 или [H⁺]=(K_w)^1/2=10^-7 моль/л.

При этом условии кривая P = f(pH) проходит через экстремум – минимум; что это действительно минимум можно убедиться еще раз продифференцировав уравнение (2.11) и установив положительное значение второй производной. Кривая титрования pH=f(y) через точку перегиба, координаты которой отвечают условиям эквивалентности.

По уравнению 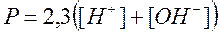можно рассчитать значения буферности и построить диаграмму буферности P=f(pH).

Таблица 2. Расчет буферности водных

растворов сильных протолитов.

[H^+] pH P=2,3([H^+]+[OH^-]) 10» 2,30 1×10^-1 1» 2,30^.10^-1 1^.10^-2 2» 2,30^.10^-2 4^.10^-3 2,4» 1,00^.10^-2 ^.............................................. 1^.10^-6 6» 2,32^.10^-6 1^.10^-7 7 4 60^.10^-7 1^.10^-8 8» 2,32^.10^-6 ^............................................ 2,5^.10^-12 11,6» 1,00^.10^-2 1^.10^-12 12» 2,30^.10^-2 1^.10^-13 13» 2,30^.10^-1 1^.10^-14 14» 2,30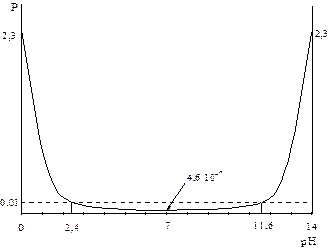
	Рис. 2.1. Диаграмма буферности водных растворов сильных протолитов.

Как видно, при добавлении щелочи к раствору сильной кислоты буферность сначала уменьшается, достигая минимального значения 4,6^.10^-7 при pH=7, затем снова возрастает, причем в широком интервале pH от 2,4 до 11,6 буферность имеет весьма низкое значение (менее 0,01).

Согласно диаграмме бу-ферности, кривая титрования pH=f(y) S-образной формы с быстрым изменением рН (скачком рН) в области 2,4 – 11,6 единиц и точкой перегиба с координатами pH=7 и y=C0 (рис.2.2). При уменьшении исходной концентрации анали-зируемой кислоты скачок становится более размытым, поэтому минимальные опреде-ляемые концентрации порядка
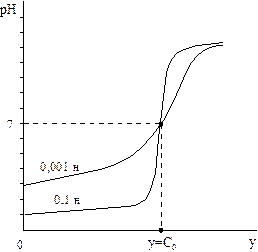
10^-4 моль/л.	Рис.2.2. Кривые титрования сильной кислоты различной концентрации сильным основанием

Нейтрализации смесей сильных кислот, полностью диссоциирующих в водной среде, отвечает та же диаграмма буферности и та же форма кривой титрования с одним скачком рН, регистрируя который можно определить лишь суммарное содержание кислот в растворе.

Нейтрализация слабой кислоты сильным основанием характеризуется тем, что концентрация анионов в ходе титрования не остается постоянной. Если воспользоваться уравнением константы диссоциации слабой кислоты в виде

(2.12)

и учесть, что концентрация непродиссоциировавшей кислоты [HA]=C₀-[A-], то можно записать

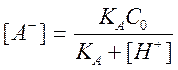(2.13)

Подставляя полученное выражение в уравнение электронейтральности(2.4), получим уравнение кривой титрования слабой кислоты сильным основанием

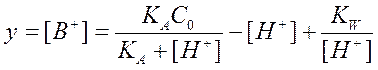(2.14)

Это уравнение третьей степени и точный расчет [H⁺] затруднен.

На практике поступают обычно проще. В начальный момент титрования, когда y = 0, справедливо равенство

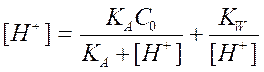(2.15)

Т.к. , то (2.16)

Решая это квадратное уравнение, имеем

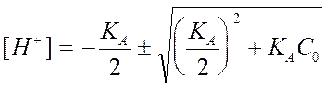(2.17)

Если С₀>>К_А, то до начала титрования

(2.18)

Для недотитрованных растворов, когда y< C₀, концентрацию ионов водорода рассчитывают, используя уравнение константы диссоциации

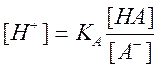(2.19)

Пренебрегая диссоциаций слабой кислоты в присутствии ее соли, можно считать, что равновесная концентрация [HA]»[недотитрованной кислоты], а равновесная концентрация анионов [A^-]» [образовавшейся соли]. Тогда

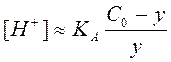(2.20)

или

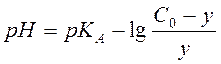(2.21)

В точке эквивалентности, когда y=C₀, вследствие гидролиза соли

В⁺А^- + H₂O = HA + B⁺OH^-

раствор будет не нейтральным, а щелочным. Концентрация ионов водорода может быть вычислена по известному уравнению

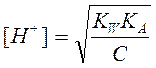(2.22)

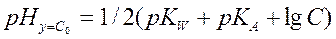(2.23)

Концентрацию соли С в эквивалентной точке можно приравнять исходной концентрации кислоты С₀, если не учитывать разбавление раствора в ходе титрования.

Чтобы выяснить форму кривой титрования слабой кислоты и имеющиеся характерные точки на этой кривой, проанализируем уравнение кривой нейтрализации (2.14), воспользовавшись величиной буферности

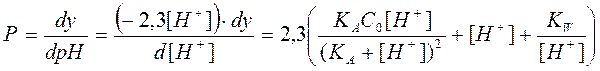(2.24)

При любых значениях рН Р ≠ 0, следовательно, кривая титрования не должна иметь экстремум. Не проводя расчетов буферности, выясним как будет вести себя зависимость P=f(pH). Для этого необходимо продифференцировать уравнение (2.24) по рН. Учитывая, что в области недотитрованных (y<C₀) растворов слабой кислоты (К_А ≤10^-5) выполняется неравенство

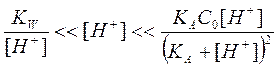(2.25)

уравнение (2.24) можно записать в виде

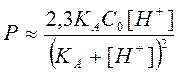(2.26)

Дифференцируя последнее выражение по рН, получим

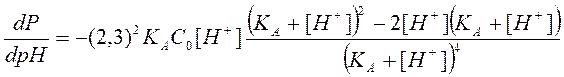(2.27)

Производная dP/dpH=0, если [H⁺]= K_A или pH= pK_A. Этому значению pH на кривой P=f(pH) отвечает максимальное значение буферности P_max, котороесогласно уравнению (2.26) имеет значение

(2.28)

и не зависит от силы кислоты, а определяется только ее концентрацией.

Равенство [H⁺]= K_A, в соответствии с уравнением (2.20), отвечает условию y=0,5C₀, т.е. полуоттитрованному раствору слабой кислоты. Если, например, сильным основанием титруется 0,1 н. слабая кислота, у которой К_А=10^-5, то изменение буферности системы в ходе титрования можно представить в виде кривой abdefg, приведенной на рис. 2.3. В данном случае наблюдается два участка повышенной буферности, первый из которых (bde) соответствует области недотитрованного раствора и обусловлен присутствием слабой кислоты и ее соли, а второй участок (fg) − избытком титранта.

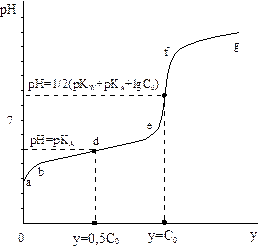
Рис. 2.3. Изменение буферности при титровании слабой кислоты сильным основанием	Рис. 2.4. Кривая титрования слабой кислоты (КА=10^-5)сильным основанием

Согласно диаграмме буферности на кривой титрования pH =f (y) слабой кислоты, представленной на рис. 2.4, полуоттитрованному раствору, отвечает точка перегиба, с ординатой рН=р К_А. Последнее равенство позволяет достаточно просто определять методом потенциометрического титрования концентрационные константы слабых кислот.

Протяженность участков низкой буферности, наблюдающихся в начале (участок ab) и в конце титрования (участок ef), зависит от силы кислоты. Чем слабее кислота (чем меньше К_А), тем больше изменения рН в начале титрования и тем меньше протяженность участка низкой буферности (ef), который обуславливает величину скачка на кривой титрования.

На рис. 2.5 представлены кривые титрования трех слабых кислот: хлоруксусной, уксусной и дихлорфенола, р КА которых равны соответственно 2,81, 4,76 и 7,85. С уменьшением силы указанных кислот величина скачка рН уменьшается, а рассчитанное с учетом гидролиза рН в точке эквивалентности увеличивается. Если константы диссоциа-ции кислот малы, то в точке эквивалентности вообще не наблюдается скачка потенциала или перегиба на кривой титрования. Возникает вопрос −

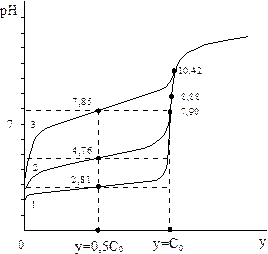
− какое минимальное значение константы диссоциации может иметь кислота, чтобы ее содержание можно было определить титрованием в водной среде?

Рис. 2.5. Кривые титрования слабых кислот: 1)−хлоруксусная (рКА=2,81); 2)−уксусная (рКА=4,76); 3−2,4 дихлорфенол (рКА=7,85)

Допустим, мы титруем слабую кислоту и добавили такую порцию титранта, когда нейтрализованной оказалась 0,1% первоначального количества кислоты. Тогда, согласно уравнению (2.21)

.

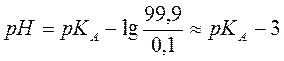Титрование можно считать законченным, если оттитровано 99,9 % (максимальная точность объемного анализа) исходной кислоты. Тогда рН анализируемого раствора

.

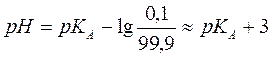Таким образом, при определении слабой кислоты с точностью 0,1%, мы должны учитывать, что изменение рН раствора в ходе титрования составляет 6 единиц

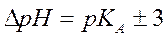. (2.29)

Если титруется 0,1 н. кислота с р К_А= 8,6, то она практически полностью будет нейтрализована при рН=11,6. Рассчитав для данного рН по уравнению (2.24) буферность системы, образованной слабой кислотой и сильным основанием, можно убедиться, что значение буферности практически будет равно 0,01. В этом случае участок (ef, рис. 2.3) с пониженной буферностью отсутствует, поэтому скачок рН в области точки эквивалентности отсутствует и на кривой титрования можно зарегистрировать только точку перегиба. Таким образом, количественное определение слабой кислоты в водных растворах с точностью 0,1% возможно, если выполняется условие

. (2.30)

Более слабые кислоты в водной среде титрованием определить невозможно.

Т.к. в уравнение буферности (2.24) входит концентрация кислоты С₀, то более точно условие определимости можно записать в виде

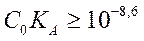. (2.31)

Если удовлетворяет точность анализа 1%, то условие возможности определения слабой кислоты в водных растворах можно записать следующим образом

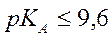(2.32)

или с учетом исходной концентрации кислоты

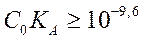(2.33)

Титрование смесей протолитов наиболее удобно проводить потенциометрическим методом, поскольку он позволяет обеспечить их раздельное опре­деление в водной и неводной средах.

Если раствор в сравнимых концентрациях содержит несколько кис­лот различной силы, то при алкалиметрическом титровании эти кис­лоты взаимодействуют с сильным основанием в порядке увеличения рК_А. Рассмотрим случай, когда в воде титру­ют смесь двух одноосновных кислот HA₍₁₎ HA₍₂₎ различной силы, причем рК_А,1< рК_А,2, а начальная концентрация этих кислот составляет соответственно С_0,1 и С_0,2. Исходя из принципа электронейтральности раствора, будет справедливо равенство

y = [B⁺] = [A₍₁₎^-]+[A₍₂₎^-] − [H⁺] + K_w / [H⁺] (2.34)

а учитывая диссоциацию каждой из кислот, уравнение кривой титрования можно записать в виде

. (2.35)

Не проводя расчета кривой титрования [H⁺]= f(y), ограничимся рассмотрением только ее формы и имеющихся на ней характерных точек. Продифференцируем уравнение (2.35) по рН и получим выражение буферности

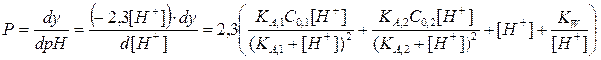(2.36)

из которого следует, что буферность свойство аддитивное и определяется присутствием всех протолитов в растворе.

Допустим, что константа диссоциации в воде более сильной кислоты К_А,1 =10^-4,5 (рК_А,1 =4,5), а более слабой − К_А,2 =10^-8,5 (рК_А,2 =8,5). Если задаваться различными значениями [H⁺], то можно рассчитать изменение буферности раствора смеси кислот в ходе титрования сильным основанием, которое описывается кривой, представленной на рис. 2.6. На даннойдиаграмме имеется две области с повышенной буферностью, которые обусловленыприсутствием в анализируемом растворе двух буферных систем, образованных слабыми кислотами и их солями. При рН>11,6 высокая буферность связана с избытком титранта (сильного основания).

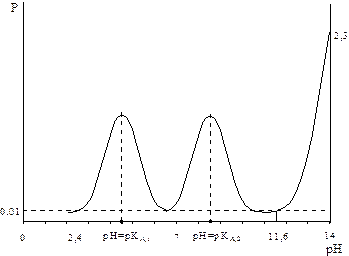
Рис. 2.6. Изменение буферности в ходе титрования водного раствора двух слабых кислот сильным основанием	Рис. 2.7. Кривая титрования смеси двух слабых кислот сильным основанием в воде

В соответствии с изменением буферности данной системы кривая титрования (рис. 2.7) имеет четыре точки перегиба, две из которых наблюдаются при значениях рН= рК_А,1 =4,5 и рН= рК_А,2 =8,5 и отвечают полуоттитрованному состоянию каждой из определяемых кислот. Две другие точки перегиба на кривой титрования соответствуют минимальным значениям буферности системы и служат для определения конца титрования.

На практике при анализе смеси слабых протолитов важно знать ответ на три вопроса: 1) как должны различаться константы ионизации, чтобы дифференцировано определить кислоты (основания); 2)какова точность анализа;

3) как рассчитать рН раствора в точках эквивалентности.

Титрование смеси кислот (оснований) приблизительно равной силы (рис. 2.8) не позволяет дифференцировано определить содержание каждого протолита

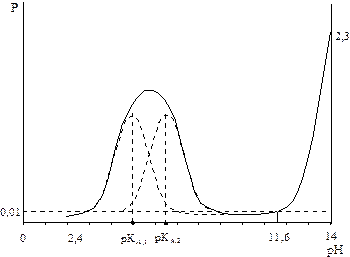
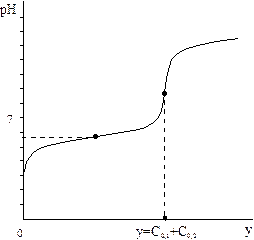
Рис. 8. Изменение буферности в ходе титрования смеси двух кислот с близкими константами диссоциации	Рис. 9. Кривая титрования смеси двух кислот с близкими константами диссоциации

Области повышенной буферности, обусловленные присутствием этих протолитов, перекрываются, а концентрация ионов водорода в каждый момент титрования соответствует суммарному содержанию всех кислот и оснований в растворе. В этом случае при определенных условиях (для наиболее слабой кислоты должны выполняться уравнения (2.30) и (2.31) на кривой титрования (рис. 2.9) наблюдается только один скачок, по которому можно определить только суммарное содержание протолитов.

Анализ смеси кислот (оснований) в водной среде возможен лишь в тех случаях, когда соответствующие константы диссоциации титруемых компонентов, как это показано на рис. 2.6, отличаются друг от друга по меньшей мере на четыре порядка:

К_А,1 / К_А,2 ≥ 10⁴ или ΔрК = рК_А,2 -рК_А,1 ≥ 4 (2.37)

В этих условиях обеспечивается достаточ­но заметное изменение потенциала индикаторного электрода вбли­зи первой точки эквивалентности и погрешность не превышает 1%, т.к. при рН= рК_А,1+ 2 будет оттитровано 99% более сильной кислоты и только 1% более слабой кислоты.

Проведение определений, при которых погрешность не превыша­ет ±0,1%, возможно при соблюдении более жестких условий:

К_А,1 / К_А,2≥ 10⁶ или ΔрК = рК_А,2 -рК_А,1 ≥ 6. (2.38)

Если концентрации анализируемых кислот существенно различаются, то условия их дифференцированного определения необходимо записать в виде

С_0,1К_А,1 : С_0,2К_А,2 ≥10⁶, (2.39)

при этом для наиболее слабой должно выполняться уравнение (2.31):

С_0,2К_А,2 ≥10^-8,6.

Для того чтобы у точки эквивалентности появился скачок (или надежно регистрируемая точка перегиба) требуются 6 единиц шкалы рН. При наличии на кривой титрования 2 скачков у двух точек стехио­метричности требуется 12 единиц рН. Однако нормальная шкала рН водных растворов имеет всего только 14 единиц рН. Следовательно, не превышая погрешности ±0,1%, в водных растворах последовательно можно титровать не более двух протолитов.

Если известны константы ионизации кислот, можно легко рассчитать ошибку их определения и рН для обеих точек стехиометричности.Когда в растворе присутствует две кислоты, то уравнение (2.12) справедливо для каждой из них

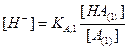и 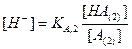. (2.40)

Концентрация иона водорода в обоих уравнениях одна и та же величина, поэтому можно написать равенство

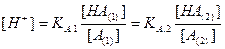. (2.41)

Другим словами, в любой момент титрования смеси двух кислот выполняется уравнение

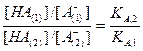. (2.42)

Если пренебречь диссоциацией слабой кислоты в присутствии ее соли, то равновесную концентрацию молекулярной формы кислоты можно считать концентрацией не нейтрализованной кислоты, а равновесную концентрацию аниона − концентрацией нейтрализованной кислоты.

Допустим, что К_А,1 ≥ К_А,2, С_0,1= 1, 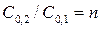и к исходной смеси добавлено количество щелочи эквивалентное содержанию более сильной кислоты. В этот момент, поскольку отношение К_А,1 / К_А,2 конечная величина, некоторое количество более сильной кислоты z будет не нейтрализовано и соответствующее количество щелочи пойдет на нейтрализацию более слабой кислоты. Величина z будет определять ошибку анализа, используя которую, уравнение (2.41) можно записать в виде

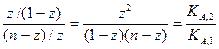. (2.43)

Т.к. на практике интересуют случаи, когда 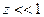, то для расчета абсолютной ошибки используют уравнение

(2.44)

из которого следует, что ошибку анализа определяют не только константы ионизации, но концентрации протолитов. Причем, чем больше концентрация более слабой кислоты, тем больше ошибка.

Расчет рН характерных точек кривой титрования смеси слабых кислот (рис. 2.7) проводят следующим образом. В начальной точке (y =0) рН титруемого раствора определяется протолизом наиболее сильной кислоты HA₍₁₎ согласно уравнению (2.18)

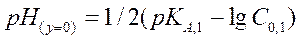(2.45)

Когда оттитрована половина более сильной кислоты (y=¹/₂C_0,1) рН=рК_{А, 1} .

Для первой точке стехиометричности (y =C_0,1) рН раствора можно рассчитать из уравнения (2.41), которое с учетом абсолютной ошибки определения z можно переписать в виде

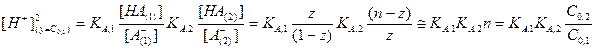
или

(2.46)

Логарифмируя, получим

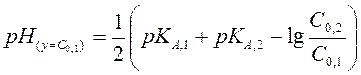(2.47)

Если С_0,1=С_0,2, то

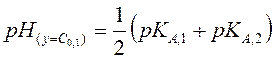(2.48)

Когда оттитровано половина более слабой кислоты (y=C_0,1+0,5C_0,2) рН = рК_{А,2 .} Для второй точки эквивалентности рН рассчитывают по уравнению (2.22), используя константу диссоциации более слабой кислоты

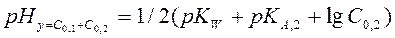(2.49)

При определении концентраций сильной и слабой кислоты в их смеси точность анализа зависит от константы диссоциации последней. С точно­стью ±0,1 % концентрацию каждой из кислот можно установить лишь в том случае, когда для слабой кислоты выполняется условие

10^-5,4 ≥ С_0,2К_А,2 ≥10^-8,6 или 5,4 ≤ рК_А,2-lgC_0,2 ≤ 8,6(2.50)

Анализ с погрешностью ±1 % может быть выполнен при условии

10^-4,4 ≥ С_0,2К_А,2 ≥10^-9,6 или 4,4 ≤ рК_А,2-lgC_0,2 ≤ 9,6 (2.51)

Изменение буферности в ходе титрования смеси сильной и слабой кислот и кривая титрования представлены, соответственно, на рис. 2.10 и 2.11.

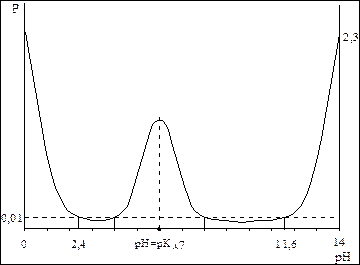
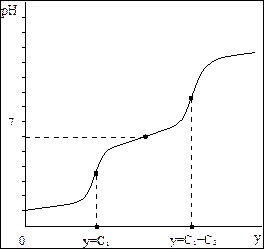
Рис. 2.10. Изменение буферности в ходе титрования смеси сильной и слабой кислот сильным основанием	Рис. 11. Кривая титрования смеси сильной и кислот сильным основанием

Многоосновную кислоту можно рассматривать как смесь двух или большего числа слабых кислот с идеально одинаковыми концентрациями. Поэтому при титровании многоосновных кислот остаются в силе уравне­ния (2.34) — (2.45), только константы диссоциации кислот К_А смеси следует заменить константами ступенчатого равновесия многоосновных кислот k_A, т.е. рК_А,1 следует заменить показателем pk_A,1, рK_А,2 − показателем рk_A,2 и рК_{А, 3} − показателем pk_A,3. В ка­честве примера на рис. 2.12 представлена кривая изменения буферности, а на рис. 2.13 кривая титрования фосфор­ной кислоты (с₀ = 0,3 моль/л).

Последовательные стадии диссоциации фосфорной кислоты имеют свои константы равновесия:

H₃PO₄ = H⁺ + H₂PO₄^-, k_A,1 = 7,5∙10^-3, pk_A,1 = 2,1;

H₂PO₄^- = H⁺ + HPO₄^2-, k_A,2 = 6,3∙10^-8, рk_A,2 = 7,2;

HPO₄^2- = H⁺ + PO₄^3-, k_A,3 = 4,0∙10^-13, pk_A,3 = 12,4.

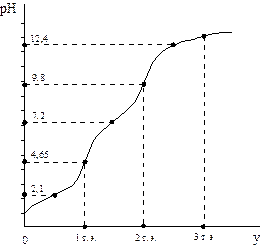
Рис. 2.12. Изменение буферности водного раствора фосфорной кислоты (с=0,3 моль/л) в ходе титрования сильным основанием	Рис.2.13. Кривая титрования фосфорной кислоты сильным основанием

В соответствии с (36) уравнение буферности трехосновной фосфорной кислоты должно иметь вид

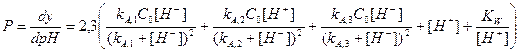, (2.52)

а кривая, рассчитанная по этому уравнению и представленная на рис. 12, имеет две точки максимума, отвечающие условию рН= pk_A,1 и pH= pk_A,2. Третий участок высокой буферности, отмеченный пунктиром и обусловленный системой HPO₄^2-/PO₄^3-, перекрывается участком повышенной буферности, вызванной появлением избытка титранта − ионов ОН^-. В связи с этим на кривой титрования наблюдается только два скачка. Первый из них наблюдается у первой точки стехиометричности, когда нейтрализован первый протон из трех. Так как рk_A,2 - pk_A,1 = 5,1, то погрешность определения кислоты по первому скачку, согласно уравнения (44), будет составлять 0,29%. рН первой точки эквивалентности рН_1т.э.=¹/₂(2,1+7,2)=4,65.

У второй точки стехиометричности также имеется скачок, практически одинаковый с первым, т.к. pk_A,3 - рk_A,2 = 5,2. Ориентируясь на вторую точку эквивалентности, для которой рН_2т.э.= ¹/₂(7,2+12,4)=9,8 можно определить концентрацию H₃PO₄ c погрешностью 0,25%. У третьей точки стехиометричности скачка нет, поскольку pk_A,3> 9,6. Таким образом, концентрацию фосфорной кислоты с одинаковым успехом можно определить используя первый или второй скачок на кривой титрования.

На практике при анализе многоосновных кислот встречаются самые разнообразные случаи. Например, на кривых титрования двухосновных винной (pk_A,1 =2,98; pk_A,2 =4,34) или щавелевой (pk_A,1 =1,23; pk_A,2 =4,12), а также трехосновной лимонной кислоты (pk_A,1 =3,1; pk_A,2 =4,75; pk_A,3 =5,4) имеется только один скачок, соответствующий переходу к средней соли. На кривой титрования двухосновной угольной кислоты (pk_A,1 =6,37; pk_A,2 =10,25), также имеется только один скачок, который соответствует переходу кислоты в кислую соль. Поэтому при титровании многопротонных кислот, чтобы не допустить ошибок в расчете концентраций и выбрать оптимальные условия анализа, необходимо знать ступенчатые константы диссоциации.

При расчете кривых титрования оснований кислотами, общий подход остается тем же, что и для слабых кислот, но удобнее вместо рН использовать величину рОН.

Дата добавления: 2014-01-07