Связка плоскостей

Лекция 13.

Собственной связкой плоскостей называется множество всех плоскостей, проходящих через одну точку (центр связки).

Несобственной связкой плоскостей называется множество всех плоскостей, компланарных одной прямой.

Теорема 1. Для того чтобы 4 плоскости, заданные относительно общей декартовой системы координат уравнениями

,

,

,

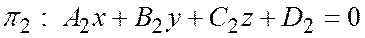(1)

принадлежали одной связке, (собственной, или несобственной) необходимо и достаточно, чтобы определитель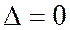

Доказательство необходимости. Дано: четыре плоскости (1) принадлежат одной связке. Требуется доказать, что .

Если 4 данные плоскости принадлежат одной собственной связке, то, обозначая через центр этой связки, будем иметь.

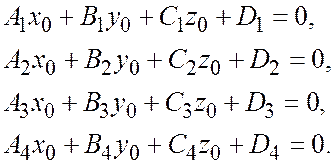
Таким образом, столбцы определителя 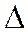линейно зависимы, значит, он равен нулю.

Далее. Если 4 данные плоскости, заданные уравнениями (1), принадлежат одной несобственной связке, то существует ненулевой вектор 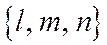компланарный всем этим плоскостям, и, значит,

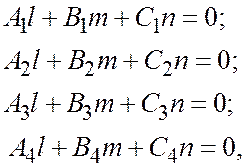
так что первые три столбца определителя 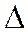линейно зависимы, а значит .

Доказательство достаточности. Дано 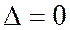. Требуется доказать, что четыре плоскости (1) принадлежат одной связке.

Если ранг матрицы

равен трем, то среди четырех данных плоскостей есть три такие, которые имеют единственную общую точку .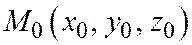

Пусть, например

тогда это будут три первые плоскости.

Первые три строки матрицы

линейно независимы, а так как , то последняя строка есть линейная комбинация первых трех:

Отсюда следует тождество, справедливое для всех х, у, z:

Из этого тождества следует, что точка 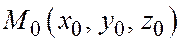, являющаяся пересечением первых трех плоскостей, лежит и на четвертой плоскости, т.е. четыре данные плоскости принадлежат одной собственной связке.

Если (отсюда уже следует, что ), то среди главных векторов 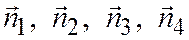данных плоскостей есть не более двух линейно независимых.

Пусть это будут векторы и 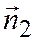и они линейно независимы, следовательно неколлинеарны, а векторы 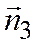и - их линейные комбинации, то есть:

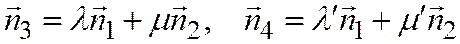. (2)

Система уравнений

имеет ненулевое решение (т.к. векторы и линейно независимы),

(например, ).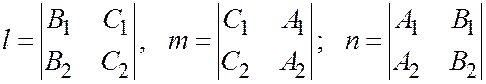

В силу соотношения (2) будем также иметь

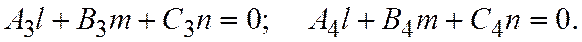
Действительно. Соотношение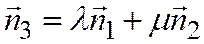

означает, что

То есть

или, сложив

но справа круглые скобки равны нулю, поэтому

Аналогично доказывается, что 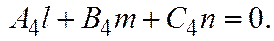Т.е. четыре данные плоскости принадлежат одной несобственной связке, т.к. ненулевой вектор всем им компланарен.

Если наконец, ранг матрицы 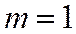, то четыре данные плоскости коллинеарны, а значит также принадлежат одной связке.

Теорема 2. Пусть в ОДСК три плоскости заданы общими уравнениями

, ,

, (3)

не принадлежащие одному пучку. Для того чтобы плоскость

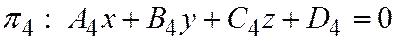(4)

принадлежала связке, определяемой плоскостями необходимо и достаточно, чтобы левая часть уравнения была линейной комбинацией левых частей уравнений :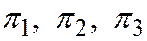

(т.е. соотношение (5) - есть тождество при всех значениях х, у, z).

Доказательство необходимости. Дано: плоскость входит в связку, определяемую плоскостями 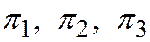. Требуется доказать, что существуют такие числа и , при которых соотношение (5) является тождеством.

Так как плоскости 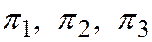не входят в один пучок, то ранг матрицы

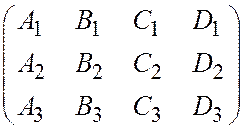
равен трем, а так как плоскость 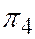входит в связку, определяемую плоскостями то

(6)

отсюда следует, что четвертая строка этого определителя есть линейная комбинация первых трех

(7)

поэтому соотношение (5) - есть тождество относительно х, у, z.

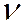Доказательство достаточности. Предположим, что существуют такие и , при которых соотношение (5) - есть тождество относительно х, у, z. Требуется доказать, что плоскость 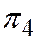входит в связку, определяемому плоскостями .

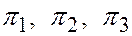Если соотношение (5) - есть тождество относительно х, у, z, то из него следуют равенства: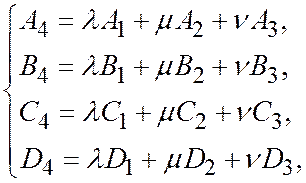

а, следовательно , т.к. четвертая строка определителя 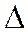есть линейная комбинация трех первых. Но если , то четыре плоскости, заданные уравнениям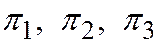и и принадлежат одной связке. Ч.т.д.

Уравнение

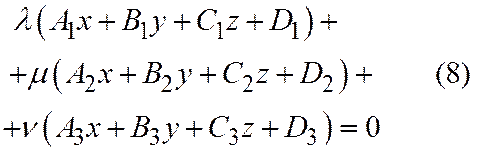
в котором хотя бы одно из чисел 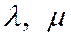, 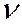не равно нулю, а

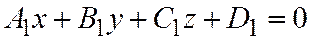
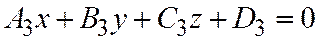(9)

общие уравнения трех плоскостей, заданных относительно общей декартовой системы координат и не принадлежащих одному пучку, называется уравнением связки плоскостей, определяемой тремя данными плоскостями.

Дата добавления: 2014-01-07