Расщепление энергетических уровней атомов в магнитном поле

Магнитный резонанс

Лекция 16.

Электронный парамагнитный резонанс (ЭПР). Идентификация и определение концентрации свободных радикалов методами ЭПР.

Ядерный магнитный резонанс (ЯМР). Принципы и диагностические возможности магнито-резонансной томографии (МРТ).

В этой главе, как и в предыдущей, рассматриваются явления, связанные с излучением и поглощением энергии атомами и молекулами

Магнитный резонанс — избирательное поглощение электромагнитных волн веществом, помещенным в магнитное поле.

В было показано, что на контур с током, помещенный в магнитное поле, действует момент силы. При устойчивом равновесии контура его магнитный момент совпадает с направле­нием вектора магнитной индукции. Такое положение занимает контур с током, предоставленный самому себе. Существенно иначе ориентируются в магнитном поле магнитные моменты частиц. Рассмотрим этот вопрос с позиции квантовой механики.

Ранее отмечалось, что проекция момента импульса электрона на некоторое направление принимает дискретные значения.

Чтобы обнаружить эти проекции, необходимо каким-то образом выделить направление Z. Один из наиболее распространенных способов — задание магнитного поля, в этом случае определяют проекцию орбитального момента импульса [см. (23.26)], проекцию спина (23.27), проекцию полного момента импульса электро­на [см. (23.30)] и проекцию момента импульса атома L_Az [см. (23.37)] на направление вектора магнитной индукции .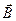

Связь между моментом импульса и магнитным моментом (13.30) и (13.31) позволяет использовать перечисленные формулы для нахождения дискретных проекций соответствующего магнитного момента на направление вектора 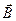. Таким образом, в отличие от классических представлений, магнитные моменты частиц ориентируются относительно магнитного поля под некоторыми определенными углами.

Для атома, например, из (23.37) получаем следующие значения проекций магнитного момента p_mz на направление вектора магнитной индукции:

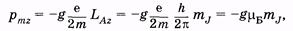(25.1)

где m_Б = e h /(4p m) — магнетон Бора (см. § 13.1), m — масса электрона, m_J — магнитное квантовое число, g — множитель Ланде (g-фактор) (см. § 13.4), для заданного уровня энергии атома он зависит от квантовых чисел L, J, S. Знак «-» в (25.1) обусловлен отрицательным зарядом электрона.

Энергия атома в магнитном поле с учетом того, что в отсутствие поля энергия атома равна Е ₀, определяется формулой

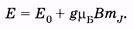(25.2)

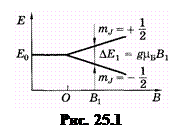Так как магнитное квантовое число m_J [см. (23.37)] может принимать 2 J + 1 значений от + J до - J, то из (25.2) следует, что каждый энергетический уровень при помещении атома в магнитное поле расщепляется на 2 J +1 подуровней. Это схематически показано на
рис. 25.1 для J = 1/2. Разность энергий между соседними подуровнями равна

D Е = g m_Б В. (25.3)

Расщепление энергетических уровней приводит и к расщеплению спектральных линий атомов, помещенных в магнитное поле. Это явление называют эффектом Зеемана.

Запишем выражение (25.2) для двух подуровней Е ₁ и Е ₂, образованных при наложении магнитного поля:

,

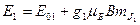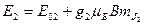, (25.4)

где Е ₀₁ и Е ₀₂ — энергетические уровни атома в отсутствие магнитного поля. Используя (23.31) и (25.4), получаем выражение для излучаемых атомом частот:

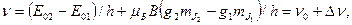(25.5)

где

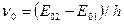(25.6)

— частота спектральной линии в отсутствие магнитного поля;

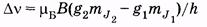(25.7)

— расщепление спектральной линии в магнитном поле. Из (25.7) видно, что Dn зависит от магнитного квантового числа, множителя Ланде и магнитной индукции поля. Если g _l = g ₂ = g, то

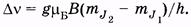
Согласно правилам отбора для магнитного квантового числа, имеем

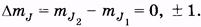(25.8)

Это соответствует трем возможным частотам:
n₀ + g m_Б B / h, n₀, n₀ - g m_Б B / h, т. е. в магнитном поле спектральная линия расщепляется и превращается в триплет (рис. 25.2). Такое расщепление называется нормальным или простым эффектом Зеемана. Он наблюдается в сильных магнитных полях или при
g ₁ = g ₂.

В слабых магнитных полях при g ₁ ¹ g ₂ существует аномальный эффект Зеемана, и расщепление спектральных линий значительно более сложное.

Дата добавления: 2014-01-07