Прямоугольный волновод

Будем считать, что проводимость стенок волновода равна бесконечности. Заряды и токи в волноводе также отсутствуют. Поле внутри волновода удовлетворяет уравнению Максвелла

,

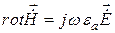, (19.4)

и граничным условиям.

Основным граничным условием является равенство нулю тангенциальной компоненты поля на стенках волновода, т.е.

(19.5)(2*)

при 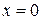, , рис. 19.7.

Рис.19.7. Прямоугольный волновод

Учитывая общую формулу для ротора произвольного вектора в прямоугольной системе координат

, (19.6) (3)

найдем выражение для проекций уравнений Максвелла, в предположении, что колебания имеют гармонический характер. Волна в волноводе при этом будет иметь вид

. (19.7) (4)

Производная поля по переменной z

. (19.8) (5)

Как дальше будет видно, постоянная распространения в волноводе (аналог волнового числа) может быть и чисто мнимой и вещественной величиной.

Производная по t

. (19.9) (6)

Учитывая эти выражения для производных, получим уравнения Максвелла в проекциях для комплексных амплитуд полей (общий множитель слева и справа в этих уравнениях можно сократить):

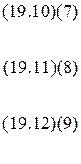
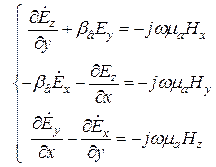
Эта система уравнений позволяет поперечные компоненты поля 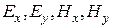выразить через продольные. Действительно подставим в уравнение (7) значение из уравнения (19.14)(11)

.

Аналогично подставим (19.13) (10) в (19.11) (8), затем (19.10) (7) в (19.14) (11), (19.11) (8) в (19.13) (10). В результате находим

(19.16) (13)

где

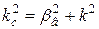, . (19.17)

Из вида этих уравнений следует вывод, что если продольные компоненты отсутствуют (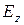и 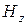), то и поперечные (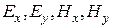) равны нулю. Т.е. чисто поперечные волны (волны типа «Т») (как в пустом пространстве), у которых 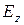и 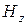равны нулю, в волноводе существовать не могут.

Если предположить в (19.16) (13), что 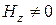, а , то имеем волну типа «Н» (Н - волну) с такими значениями напряженности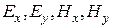

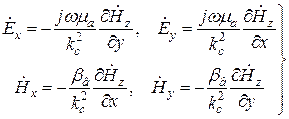(19.18) (14)

Соответственно, положив в формулах (19.16) (__),,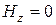 получим значения напряженности полей 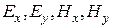для волны типа «Е» (Е -волны).

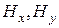Если подставить из (19.16) (13) в (19.15) (12) и из (19.10) (7) в (19.14) (11), то получим такие две независимых между собой системы уравнений, являющихся волновыми уравнениями Гельмгольца

, (19.19) (15)

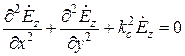. (19.20) (16)

Независимость этих уравнений свидетельствует о том, что решения для Н -волн и Е -волн можно искать независимо, и что эти типы волн могут в волноводе существовать независимо.

Для того чтобы найти эти волны, необходимо прежде всего решить уравнения (19.19) (15), (19.20) (16) при наличии граничных условий (19.5) (2*).

Решения этих уравнений обычно находят методом разделения переменных. Найдем решение уравнения(19.19) (15), представив его в виде

. (19.21) (17)

Подставив это предполагаемое решение в уравнение в (19.19) (__), получим:

,

или

. (19.22) (18)

В уравнении (19.22) (18) переменные x, y и зависящие от них функци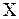и и 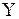разделены. Равенство слагаемых в этом уравнении постоянной величине возможно, лишь в случае равенства константам каждого из слагаемых, т.е.

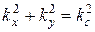, , . (19.23) (19)

Это два простейших волновых уравнения, которые целесообразно записать в виде:

.

. (19.24) (20)

Общие решения этих двух обыкновенных дифференциальных уравнений известны

,

, , (19.25) (21)

,

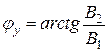, . (19.26) (22)

Тогда на основании (19.21) (11)

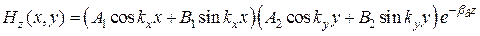. (19.27) (23)

Разберемся теперь с граничными условиями. Как отмечалось, тангенциальные компоненты электрических полей на стенках волновода должны быть равны нулю, т.е.

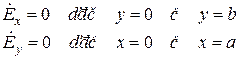(19.28) (24)

Подставив нулевые значения этих полей в выражение (19.18) (14), получим дополнительные граничные условия

(19.29) (25)

.

Из условия следует, что , а из условия 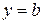, что и .

Аналогично из условия

,

следует, что , , ,

где

n =0,1,2,3…, m =0,1,2,3….

Тогда очевидно, что

. (19.30) (26)

Так как

, , , ,

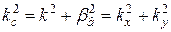то

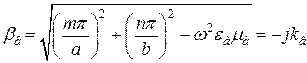, (19.31) (27)

где

.

Определяя из формулы (19.30) (26) производные , 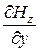и подставляя их в формулы для полей Н -волн (19.18) (14) получим следующие значения поперечных компонент полей 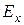, , 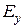, 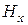(с точностью до множителя )

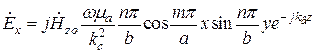, (19.32) (28)

, (19.33) (29)

,

, (19.34) (30)

, (19.35) (31)

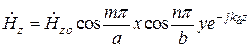(19.36) (32)

,

где 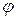- начальная фаза.

Рассмотрим функции и при m, n =1,2, рис. 19.8.

Рис.19.8. Графики функций и при m =1,2, n =1,2

Формулы (19.33–19.36)(28-32) и графики показанные на рис. 19.8, показывают при m = n =1 вдоль стенок волноводов укладываются две стоячие полуволны. При m = n =2 вдоль стенок укладываются стоячие волны с одним периодом. Далее видно, что поля с индексами m = n =0 равны нулю, т.е. такие волны в волноводе не могут существовать. Существовать в волноводе могут лишь волны, соответствующие индексам или , . Обозначают такие волны символам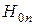и , , (или , , ). Очевидно, что если 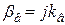является мнимой величиной, то такие волны будут распространятся в волноводе. Если же 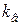- вещественная величина, то такие волны быстро затухают и распространятся в волноводе не могут.

Критическое значение частоты, при котором переходит с мнимого значения в комплексное, определяется формулой (19.31) (27), т.е.

, (19.37) (33)

или

,

. (19.38) (34)

При величина 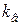- вещественна, а 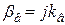- мнимая. Т.е. в волноводе могут распространятся волны лишь с частотами превышающими критичное значение частоты (19.38) (34).

Критическая длина волны

. (19.39)

Критическая частота (длина волны) тем выше (меньше), чем меньше размеры волновода «а» и «в».

Фазовая скорость в волноводе рассчитывается по известной формуле

где

, ,

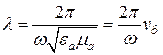а

.

Групповую скорость находим по формуле

.

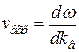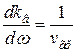Дифференцируя (19.37) (33) по и учитывая, что в соответствии с правилом дифференцирования обратной функции, находим

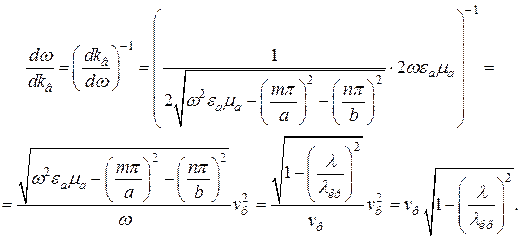
Таким образом,

(19.40)

Длина волны в волноводе

. (19.41)

Видно, что длина волны в волноводе больше длины волны 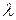в свободном пространстве с параметрами .

Дата добавления: 2014-01-07