Теорема Гаусса

Поток вектора напряженности электростатического поля.

Параллельные заряженные плоскости.

Бесконечная однородно заряженная плоскость.

Проводящая поверхностно заряженная сфера.

Применение теоремы Гаусса к расчету электростатических полей.

Поток вектора напряженности электростатического поля. Теорема Гаусса.

Вопросы

Электрическое поле в вакууме

Лекция 3

2.2. Объёмно заряженный шар.

Основной задачей электростатики является задача о нахождении напряженности 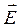и потенциала j электрического поля в каждой точке пространства. Принцип суперпозиции для заряженного тела сводится к его разбиению на малые кусочки, играющие роль точечных зарядов. Однако этот подход сопряжен с математическими трудностями.

Второй подход базируется на теореме Гаусса и упрощает расчеты и j.

Поток вектора напряженности

Поле вектора 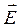характеризуется силовыми линиями напряженности:

· касательные к этим линиям характеризуют вектор 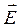по направлению;

· густота линий (количество линий, пронизывающих произвольную площадку dS) характеризует модуль Е.

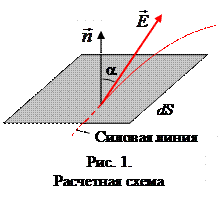
Потоком (Ф _Е) вектора 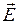электрического поля через плоскую поверхность площади 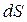называется скалярная физическая величина, характеризующая интенсивность поля в данном месте пространства и численно равная количеству силовых линий, пронизывающих данную площадку в направлении нормали к ней.

, (1)

где – напряженность электрического поля, которая предполагается постоянной в пределах площадки 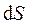; – угол между направлением вектора 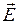и единичного вектора нормали к площадке 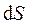. Формулу (1) можно записать для точки, используя понятие скалярного произведения векторов:

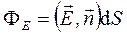. (2)

Поток вектора напряженности – величина алгебраическая (внешняя нормаль всегда направлена наружу поверхности):

Ф _Е > 0, если вектор 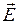направлен наружу;

Ф _Е < 0, если вектор 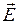направлен внутрь.

Поток Ф _Е, создаваемый единичным положительным зарядом

, (3)

площадь шара 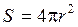, напряженность поля точечного заряда ,

.

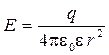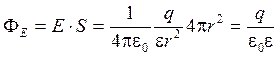Итак, 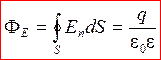. (4)

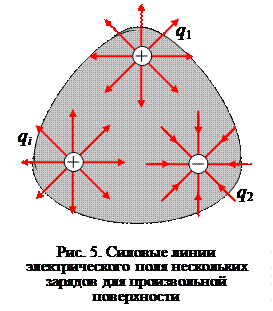
Поток вектора Ф _Е характеризует число силовых линий, пронизывающих поверхность. Для поверхности S ₂ Ф _Е =0, т.к. число входящих силовых линий равно числу выходящих.

Итак, для произвольной поверхности поток вектора Ф _Е определяется так же, как и для шаровой, по формуле (4).

Из принципа суперпозиции:

, (5)

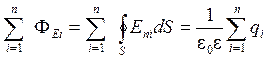, (6)

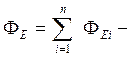полный поток через зам­кну­тую поверхность, соз­да­ва­е­мый всеми зарядами.

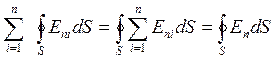. (7)

Теорема Гаусса: 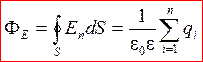. (8)

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ee₀.

В общем случае для непрерывно распределенного заряда с объемной плотностью r (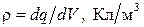) теорема Гаусса принимает вид:

. (9)

Дата добавления: 2014-01-07