Теорема 1 Шаля для ориентированных углов

Углы

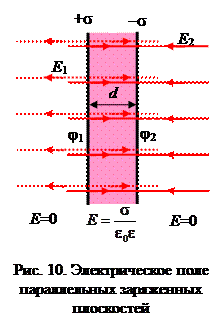
Параллельные заряженные плоскости

По принципу суперпозиции:

Þ

внутри объёма , вне объёма . (16)

Разность потенциалов

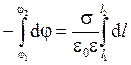Þ Þ

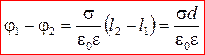. (15)

Таким образом, поле заряженных плоскостей однородно и сосредоточено в объёме между плоскостями.

Углом называется совокупность двух лучей p и q, выходящих из одной точки О. Точка О называется вершиной угла, а лучи p и q – его сторонами. Если лучи p и q совпадают, то угол называется нулевым, а если один из них является предложением другого, то угол называется развернутым.

Углы измеряются в градусах. Прямой угол . А также в радианах. Полная окружность 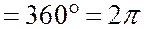радиан. 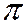- отношение длины окружности к ее диаметру.

Ориентированным углом 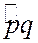называется упорядоченная пара лучей p и q, выходящих из одной точки О. Порядок сторон определяется порядком их записи: p – первая, q – вторая.

Ориентация угла (положительная или отрицательная) определяется по ориентации плоскости . На каждом из лучей берется по точке А и В, отличных от вершины О и сравнивается ориентация с ориентацией . Величине (p, q) ориентировочного угла 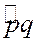лежащего на ориентированной плоскости приписывается бесконечное множество значений:

Записывается это следующим образом:

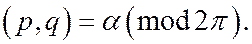
(читается так: 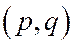сравнимо с 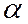по модулю 2)

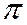Пусть p, q, r – три луча, выходящие из точки О, лежащие на ориентированной плоскости. Тогда

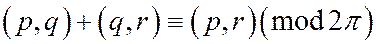(1)

Доказательство. Предложим сначала, что лучи p, q, r – попарно различны и ни один из них не является продолжением другого.

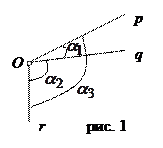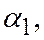
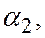
Обозначим через 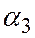соответственно главные значения углов 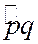; 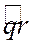и 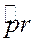(главные значения углов – это значение углов без периодов ).

Случай 1. Луч q проходит внутри угла . Тогда сумма величины угла, образованного лучами p и q, и величины угла, образованного лучами q и r, равна величине угла, образованного лучами p и r, т.е.

.

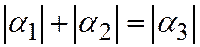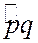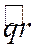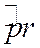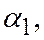
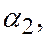
Но так как углы ; и имеют одинаковую ориентацию, то 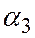- числа одного знака, а потому из последнего равенства следует, что 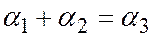и, значит,

.

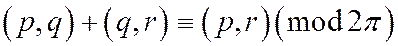Случай 2. Луч r проходит внутри угла .

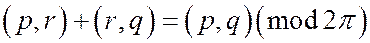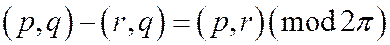Тогда, на основании уже доказанного: , или

или:

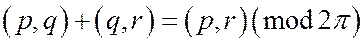, чтд.

Случай 3. Луч р проходит внутри угла

Тогда

,

,

.

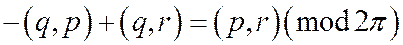Случай 4. Лучи p, q, r попарно различны, ни один из них не проходит внутри угла, образованного двумя другими и ни один из них не является продолжением другого.

В этом случае

,

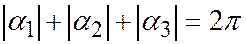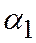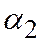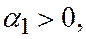
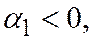
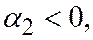
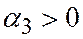причем и одного знака, а - число знака, им противоположного (для случая, изображенного на рис 2, , а для случая на рис 3, ). Таким образом имеет место одно из двух равенств 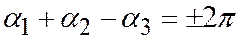или

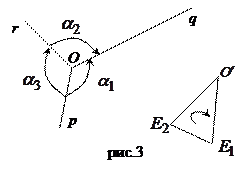
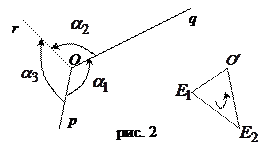Отсюда

Случай 5. Среди лучей p, q, r есть совпадающие. Пусть, например, совпадают лучи p и q. Тогда и, значит

т.е. .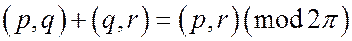

Аналогично доказывается это равенство в случае, если совпадают лучи q и r. Если же совпадают лучи p и r, то 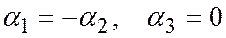и значит, опять

.

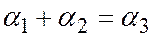Случай 6. Один из лучей p, q, r является продолжением другого. Пусть, например, луч p – продолжение луча r. Тогда либо 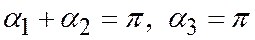, либо значит, либо 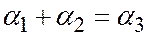, либо .

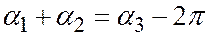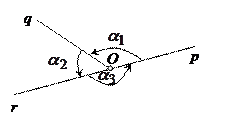
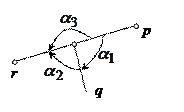
Из обоих равенств следует, что

.

Следствие. Пусть l, m, n – три луча, имеющие общую точку О и лежащие на ориентированной плоскости. Тогда

.

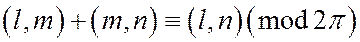Теорема 2. (Теорема Шаля для прямых)

Пусть а, b, с – три прямые, лежащие на ориентированной плоскости и имеющие общую точку О. Тогда

.

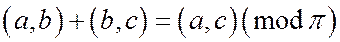Доказательство. Пусть p, q, r – соответственно лучи, лежащие на прямых а, b, с. И выходящие из точки О. На основании теоремы Шаля для углов

,

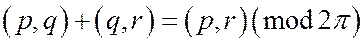следовательно,

.

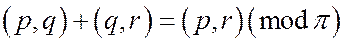Но так как какое-нибудь значение 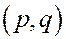есть одно из значений угла 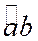, одно из значений есть одно из значений угла 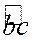, а одно из значений 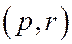есть одно из значений угла 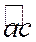, то из последнего соотношения следует, что

p

a

q

r

b

с

Дата добавления: 2014-01-07