Криволинейные координаты

До сих пор, желая знать положение точки на плоскости, или в пространстве, мы пользовались декартовой системой координат. Так, например, положение точки в пространстве мы определяли с помощью трёх координат. Этими координатами были абсцисса, ордината и аппликата переменной точки пространства. Однако ясно, что задание абсциссы, ординаты и аппликаты точки является не единственным способом определения положения точки в пространстве. Это можно сделать и иным способом, например, с помощью криволинейных координат.

Пусть по некоторому, вполне определенному правилу каждой точке М пространства однозначно соответствует некоторая тройка чисел (q ₁, q ₂, q ₃), причём различным точкам соответствуют различные тройки чисел. Тогда говорят, что в пространстве задана система координат; числа q ₁, q ₂, q ₃, которые соответствуют точке М, называются координатами (или криволинейными координатами) этой точки.

В зависимости от того правила, по которому тройка чисел (q ₁, q ₂, q ₃) ставится в соответствие точке пространства, говорят о той или иной системе координат.

Если хотят отметить, что в данной системе координат положение точки М определяется числами q ₁, q ₂, q ₃, то это записывается следующим образом М (q ₁, q ₂, q ₃).

Пример 1. Пусть в пространстве отмечена некоторая фиксированная точка О (начало координат), и через неё проведены три взаимно перпендикулярные оси с выбранным на них масштабом. (Оси Оx, Оy, Оz). Тройке чисел x, y, z поставим в соответствие точку М, такую, что проекции её радиус-вектора ОМ на оси Оx, Оy, Оz будут равны соответственно x, y, z. Такой способ установления зависимости между тройками чисел (x, y, z) и точками М приводит нас к хорошо известной декартовой системе координат.

Легко видеть, что в случае декартовой системы координат не только каждой тройке чисел соответствует определённая точка пространства, но и обратно, каждой точке пространства соответствует определённая тройка координат.

Пример 2. Пусть в пространстве снова проведены оси координат Оx, Оy, Оz, проходящие через фиксированную точку О (начало координат).

Рассмотрим тройку чисел r, j, z, где r ³0; 0£ j £2 p, –¥< z <¥, и поставим в соответствие этой тройке чисел точку М, такую, что её аппликата равна z, а её проекция на плоскость Оxy имеет полярные координаты r и j (см. рис. 4.1). Ясно, что здесь каждой тройке чисел r, j, z соответствует определённая точка М и обратно, каждой точке М отвечает определённая тройка чисел r, j, z. Исключением являются точки, лежащие на оси Оz: в этом случае r и z определены однозначно, а углу j можно приписать любое значение. Числа r, j, z называются цилиндрическими координатами точки М.

Легко установить связь между цилиндрическими и декартовыми координатами:

x = r ×cos j; y = r ×sin j; z = z.

И обратно ; ; z = z.

Пример 3. Введём сферическую систему координат. Зададим три числа r, q, j, характеризующие положение точки М в пространстве следующим образом: r – расстояние от начала координат до точки М (длина радиус-вектора), q – угол между положительным направлением оси Оz и радиусом-вектором ОМ (широта точки М) j – угол между положительным направлением оси Оx и проекцией радиус-вектора на плоскость Оxy (долгота точки М). (См. рис. 4.2).

Ясно, что и в этом случае не только каждой точке М соответствует определённая тройка чисел r, q, j, где r ³ 0, 0£ q £ p, 0£ j £2 p, но и обратно, каждой такой тройке чисел отвечает определённая точка пространства (снова за исключением точек оси Оz, где эта однозначность нарушается).

Легко найти связь между сферическими и декартовыми координатами:

x = r sin q cos j; y = r sin q sin j; z = r cos q.

; ; .

Вернёмся к произвольной системе координат (Оq ₁, Оq ₂, Оq ₃). Будем считать, что не только каждой точке пространства отвечает определённая тройка чисел (q ₁, q ₂, q ₃), но и обратно, каждой тройке чисел отвечает определённая точка пространства. Введём понятие координатных поверхностей и координатных линий.

Определение. Множество тех точек, для которых координата q ₁ постоянна, называется координатной поверхностью q ₁. Аналогично определяются координатные поверхности q ₂, и q ₃ (см. рис. 4.3).

Очевидно, что если точка М имеет координаты С ₁, С ₂, С ₃ то в этой точке пересекаются координатные поверхности q ₁= C ₁; q ₂= C ₂; q ₃= C ₃.

Определение. Множество тех точек, вдоль которых изменяется только координата q ₁ (а остальные две координаты q ₂ и q ₃ остаются постоянными), называется координатной линией q ₁.

Очевидно, что всякая координатная линия q ₁ является линией пересечения координатных плоскостей q ₂ и q ₃.

Аналогично определяются координатные линии q ₂ и q ₃.

Пример 1. Координатными поверхностями (по координате x) в декартовой системе координат являются все плоскости x = const. (Они параллельны плоскости Оyz). Аналогично определяются координатные поверхности по координатам y и z.

Координатная x -линия – это прямая, параллельная оси Оx. Координатная y -линия (z -линия) – прямая, параллельная оси Оу (оси Оz).

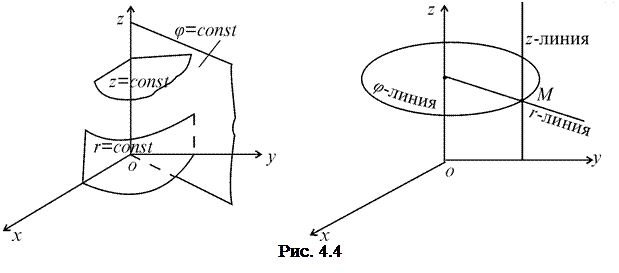
Пример 2. Координатными поверхностями в цилиндрической системе являются: любая плоскость, параллельная плоскости Оxy (координатная поверхность z = const), поверхность кругового цилиндра, ось которого направлена по оси Оz (координатная поверхность r = const) и полуплоскость, ограниченная осью Оz (координатная поверхность j = const) (см. рис. 4.4).

Название цилиндрическая система координат объясняется тем, что среди её координатных поверхностей имеются цилиндрические поверхности.

Координатными линиями в этой системе являются z -линия – прямая, параллельная оси Оz; j -линия – окружность, лежащая в горизонтальной плоскости с центром на оси Оz; и r -линия – луч, выходящий из произвольной точки на оси Оz, параллельно плоскости Оxy.

Пример 3. Координатными поверхностями в сферической системе координат служат сферы с центром в начале координат (поверхности r = const), полуплоскости, ограниченные осью Оz (поверхности j = const) и конические поверхности, с образующими, составляющими постоянный угол с положительным направлением оси Оz (поверхности q = const) (см. рис. 4.5).

Рис. 4.5

Так как среди координатных поверхностей имеются сферы, то эту систему координат называют сферической.

Координатные линии здесь таковы: r -линия – луч, выходящий из начала координат, q -линия – полуокружность с центром в начале координат, соединяющая две точки на оси Оz; j -линия – окружность, лежащая в горизонтальной плоскости, с центром на оси Оz.

Во всех рассмотренных выше примерах координатные линии, проходящие через какую-либо точку М, ортогональны друг другу. Это бывает далеко не во всякой системе координат. Однако мы ограничимся изучением только таких систем координат, для которых это имеет место; такие системы координат называются ортогональными.

Определение. Система координат (Оq ₁, Оq ₂, Оq ₃) называется ортогональной, если в каждой точке М координатные линии, проходящие через эту точку, пересекаются под прямым углом.

Рассмотрим теперь какую-нибудь точку М и проведём единичные векторы касающиеся в этой точке соответствующих координатных линий и направленные в сторону возрастания соответствующей координаты. Если эти векторы в каждой точке образуют правую тройку, то нам задана правая система координат. Так, например декартова система координат x, y, z (при обычном расположении осей) является правой. Также являются правыми цилиндрическая система координат r, j, z (но именно при таком порядке координат; если изменить порядок следования координат, взяв, например, r, z, j, мы уже не получим правой системы).

Сферическая система координат также является правой (если установить такой порядок следования r, q, j).

Заметим, что в декартовой системе координат направление единичного вектора 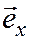не зависит от того в какой точке М мы проводим этот вектор; то же самое справедливо и относительно векторов . Иное мы наблюдаем в криволинейных системах координат: например, в цилиндрической системе координат векторы 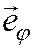в точке М и в какой-либо другой точке М ₁ уже вовсе не обязаны быть параллельными друг другу. То же относится и к вектору (в разных точках он имеет, вообще говоря, разные направления).

Таким образом, тройка единичных ортогональных векторов в криволинейной системе координат зависит от положения точки М, в которой эти векторы рассматриваются. Тройка единичных ортогональных векторов называется подвижным репером, а сами векторы – единичными ортами (или просто ортами).

Дата добавления: 2014-01-07