Линейная зависимость векторов. Линейная комбинация векторов. Коллинеарность векторов. Компланарность векторов

Лекция 6.

Векторы 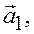…, 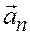называются линейно зависимыми, если существуют числа 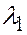, , 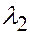… , 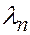среди которых по крайней мере одно, не равное нулю, такие, что

.

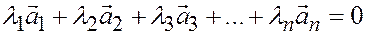Сумма произведений чисел 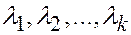на векторы 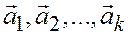, т.е. вектор

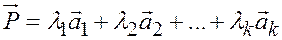
называется линейной комбинацией векторов .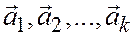

Если вектор 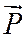представлен в виде линейной комбинации векторов 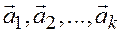, то говорят также, что вектор 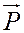разложен по векторам .

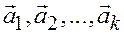Данное выше определение линейной зависимости векторов 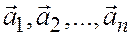, эквивалентно такому: векторы 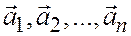линейно зависимы, если один из них можно представить в виде линейной комбинации остальных (или разложить по остальным).

Теорема 1. Для того чтобы два вектора 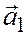и 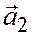были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны.

Доказательство необходимости. Дано: векторы 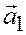и 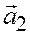линейно зависимы. Требуется доказать, что они коллинеарны. Так как векторы 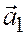и 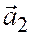линейно зависимы, то существуют числа 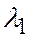и 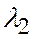, не равные нулю одновременно, и такие, что

.

Пусть, например, 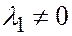; тогда

;

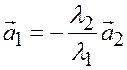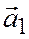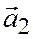отсюда следует, что векторы и коллинеарны.

Доказательство достаточности. Дано: векторы и 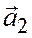коллинеарны. Требуется доказать, что они линейно зависимы.

Если 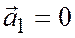, то имеет место равенство 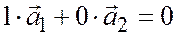, а это означает, что векторы 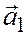и 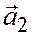линейно зависимы .

Если же 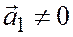, то полагая , находим 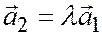, или 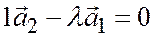; значит векторы 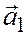и 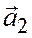линейно зависимы.

Три вектора называются компланарными, если, будучи отложены от одной точки, оказываются лежащими в одной плоскости.

Теорема 2. Для того, чтобы три вектора 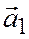, , 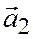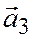были линейно зависимы, необходимо и достаточно, чтобы они были компланарны.

Доказательство необходимости. Дано: векторы , , 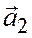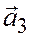линейно зависимы. Требуются доказать, что они компланарны.

Так как векторы 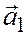, , 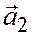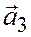линейно зависимы, то существуют числа 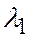, , 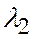, 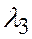среди которых есть хотя бы одно ; такие, что

.

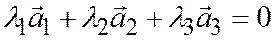Пусть, например, ; тогда

.

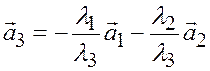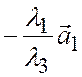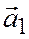Векторы и коллинеарны соответственно векторам и 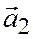; поэтому сумма таких векторов, т.е. вектор 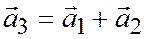будет компланарен с векторам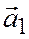и и .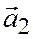

Доказательство достаточности. Дано: векторы 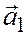, , 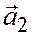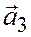компланарны. Требуется доказать, что эти векторы линейно зависимы.

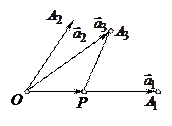Если векторы и 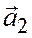коллинеарны, то они линейно зависимы (теорема 1 настоящего параграфа), т.е. найдутся числа 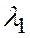и 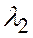, из которых по крайней мере одно не равно нулю и такие, что 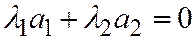, но тогда и 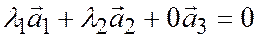, т.е. векторы 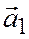, , 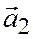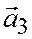линейно зависимы.

Пусть векторы 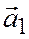и 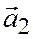неколлинеарны. Отложим векторы 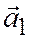, и от одной и той же точки О:

.

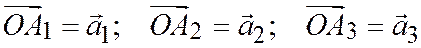Так как векторы 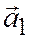, , компланарны, то точки О, 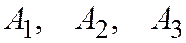лежат в одной плоскости. Спроектируем точку 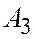на прямую параллельно прямой 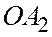; пусть Р – эта проекция. Тогда и так как

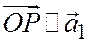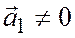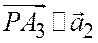и , и ,

то, полагая

,

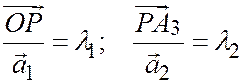находим

,

так что

,

то есть вектор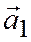ы , , - линейно зависимы.

Теорема 3. Всякие четыре вектора 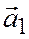, , 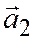, 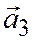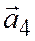в пространстве линейно зависимы.

Доказательство. Предложим, то векторы 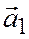, , 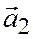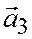некомпланарны. Отложим все векторы 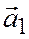, , 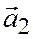, 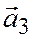от одной и той же точки О:

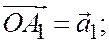
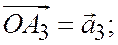
. (см.рис)

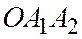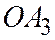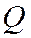Пусть Р – проекция точки на плоскость параллельно прямой , а - проекция точки Р на прямую параллельно прямой 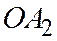. Тогда .

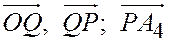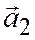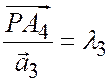Векторы соответственно коллинеарны векторам , и . Полагая ; ; получим ; ;

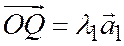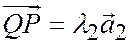и, следовательно:

,

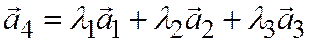т.е. вектор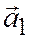ы , , , линейно зависимы.

Теорема 4. Для того, чтобы два ненулевых вектора 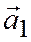и 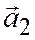были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны.

Докажем теорему для случая, когда векторы заданы своими координатами относительно общей декартовой системы координат в пространстве.

Доказательство необходимости. Дано: векторы 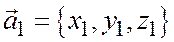; и коллинеарны. Требуется доказать, что их координаты пропорциональны.

Так как 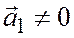, то полагая , получим 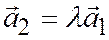, т.е.

,

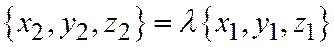или

. Ч.т.д.

Доказательство достаточности. Дано: координаты векторов

и

пропорциональны. Требуется доказать, что эти векторы коллинеарны.

Пусть 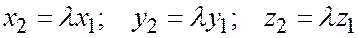; то есть , или 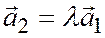, и, значит, векторы и коллинеарны.

Теорема 5. Для того, чтобы два вектора 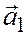и 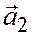, заданные своими координатами относительно общей декартовой системы координат на плоскости

,

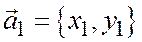или относительно общей декартовой системы координат в пространстве

;

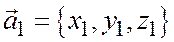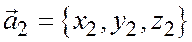
были коллинеарны, необходимо и достаточно, чтобы

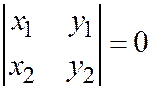(в случае плоскости),

(в случае пространства).

Докажем теорему для случая, когда векторы 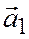и 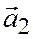заданы своими координатами относительно общей декартовой системы координат в пространстве.

Доказательство необходимости. Дано: векторы 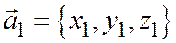и 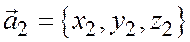коллинеарны. Требуется доказать, что выполнены соотношения

.

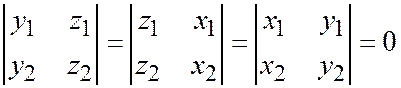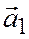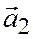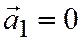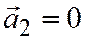Если векторы и ненулевые и коллинеарны, то их координаты пропорциональны, а потому эти равенства выполнены (определитель, в котором две строки пропорциональны, равен нулю). Если или (или ==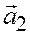0), то это равенство очевидно.

Доказательство достаточности. Дано, что эти соотношения выполнены. Требуется доказать, что векторы 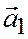и коллинеарны.

Если 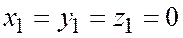(т.е. =0), то векторы и коллинеарны (т.к. нулевой вектор коллинеарен любому вектору). Пусть хотя бы одно из чисел не равно нулю, например 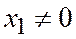. Положим ; тогда и из соотношения или (раскрывая определитель) 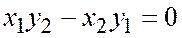, находим

,

и так как 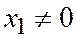имеем 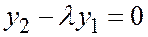, т.е. .

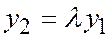Аналогично из соотношения

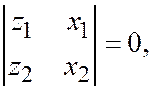или 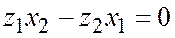, находим:

,

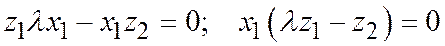и так как 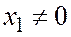, то т.е. .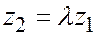

Итак, 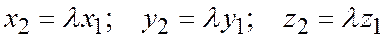или ,

т.е. векторы и 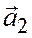коллинеарны.

Теорема 6. Необходимым и достаточным условием компланарности трех векторов

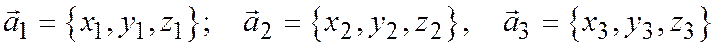заданных своими координатами относительно общей декартовой системы координат, является равенство

Доказательство. На основании предыдущей теоремы векторы , , 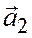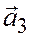будут компланарны тогда и только тогда, когда найдутся три числа 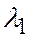, , 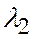, 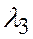не равные нулю одновременно, такие, что

,

или

,

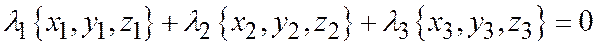или

Эта система соотношений относительно 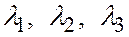линейная и однородная. Но для того, чтобы линейная однородная система n уравнений с n неизвестными имела ненулевое решение, (т.е. решение, в котором хотя бы одно из неизвестных не равно нулю), необходимо и достаточно, чтобы определитель этой системы был равен нулю, то есть чтобы определитель системы равнялся нулю.

Это и доказывает нашу теорему.

Из доказанных теорем вытекают такие следствия.

Следствие 1. Три попарно различные точки 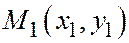, , 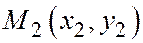, заданные своими координатами относительно общей декартовой системы координат на плоскости, лежат на одной прямой тогда и только тогда, когда векторы и 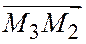коллинеарны, т.е. тогда и только тогда, когда их координаты пропорциональны:

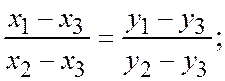или .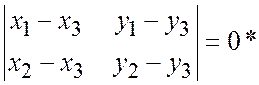

среди этих точек могут быть и совпадающие.

Следствие 2. Три попарно различные точки , , , заданные своими координатами относительно общей декартовой системы координат в пространстве, принадлежат одной прямой тогда и только тогда, когда выполнены соотношения

,

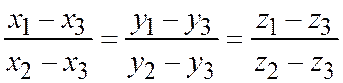или

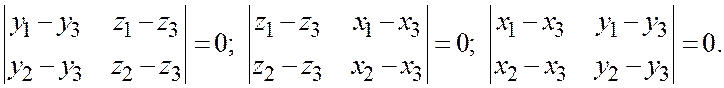
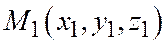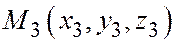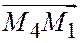Следствие 3. Точки , , , , заданные своими координатами относительно общей декартовой системы координат в пространстве, принадлежат одной плоскости тогда и только тогда, когда векторы ; ; компланарны, т.е. тогда и только тогда, когда .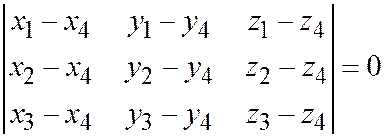

Дата добавления: 2014-01-07