Базис и координаты вектора

Базисом на плоскости называется упорядоченная пара неколлинеарных векторов 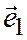, , 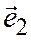лежащих в этой плоскости.

Базисом в пространстве называется упорядоченная тройка некомпланарных векторов , , .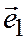

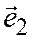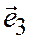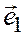Теорема 1. Всякий вектор , компланарный с двумя неколлинеарными векторами и 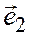, может быть и притом единственным образом разложен по этим векторам.

Доказательство существования разложения. Отложим все векторы 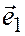, 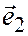и от одной и той же точки О:

; ; .

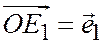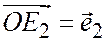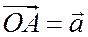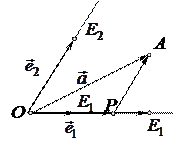Тогда, в силу компланарности векторов 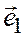, 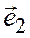и 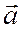, точки 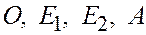лежат в одной плоскости.

Пусть Р – проекция точки А на прямую 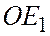параллельно прямой 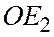(см.рис).

Тогда 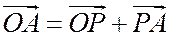, а так как векторы 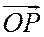и 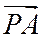соответственно коллинеарны ненулевым векторам 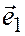и 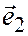, то, полагая 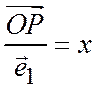; 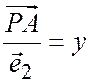, будем иметь ; .

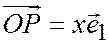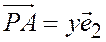Так что 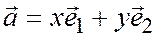ч.т.д.

Доказательство единственности разложения. Пусть существует еще другое разложение: .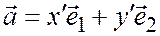

Тогда

,

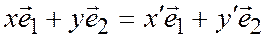или

.

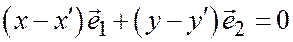Если хотя бы одна из разносте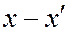й и 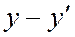была бы не равна нулю, то последнее соотношение означало бы, что векторы 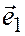и 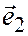линейно зависимы, а потому коллинеарны, значит

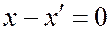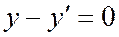; ; т.е. 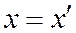, 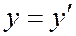ч.т.д.

Теорема 2. Всякий вектор 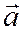пространства может быть и притом единственным образом разложен по трем некомпланарным векторам , , .

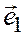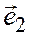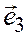Доказательство существования разложения. Отложим все векторы 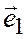, , 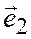, от одной и той же точки О:

; ; ; .

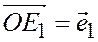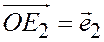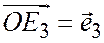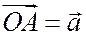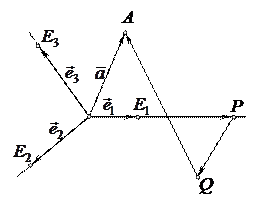Пусть Q – проекция точки А на плоскость 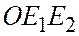параллельно прямой 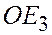, а Р – проекции точки Q на прямую 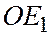параллельно прямой 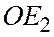(см.рис).

Так как

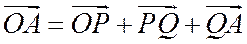
и векторы 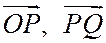, и 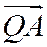соответственно коллинеарны векторам 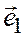, , 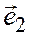, 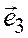то, полагая 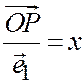; ; 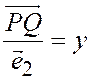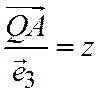, будим иметь: 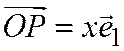; ; 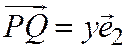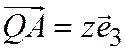, значит 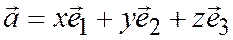. ч.т.д.

Доказательство единственности разложения. Предположим, что существует еще разложение

,

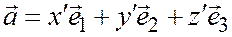тогда

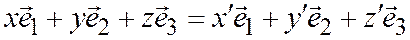
или

.

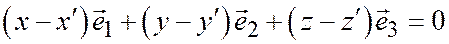Если хотя бы одна из разностей 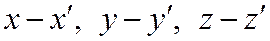была бы отлична от нуля, то последнее соотношение означало бы, что векторы 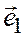, , 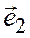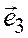линейно зависимы, а потому компланарны.

Значит 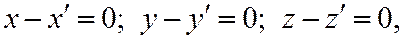то есть .

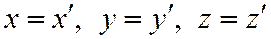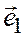Теорема 3. Коэффициенты в разложении вектора , лежащего в некоторой плоскости, по масштабным векторам и 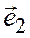общей декартовой системы координат на этой плоскости являются координатами вектора .

Доказательство. Пусть вектор 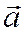лежит на плоскости, в которой введена общая декартова система координат хОу с масштабными векторам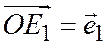и ; и .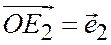

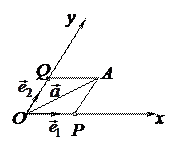Отложим вектор 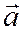от начала координат 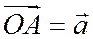и разложим его по векторам 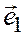и :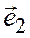

.

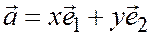Выберем на осях Ох и Оу точки Р и Q, такие, что ; .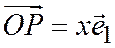

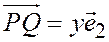Тогда 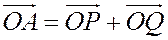и, значит, 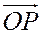- проекция вектора 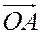на ось Ох параллельно оси Оу, а 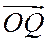- проекция вектора 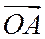на ось Оу параллельно оси Ох.

Далее из соотношения 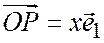; 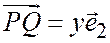следует, что 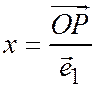; 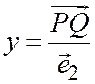, т.е. х и у – координаты вектора 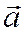ч. т. д.

Теорема 4. Коэффициенты в разложении вектора 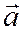по масштабным векторам 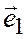, , 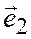общей декартовой системы координат в пространстве являются координатами вектора .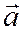

Доказательство аналогично доказательству предыдущей теоремы.

Замечание 1. Назовем радиусом – вектором произвольной точки М плоскости или пространства вектор 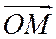, где О – фиксированная точка плоскости (или пространства). Из доказанных теорем 3 и 4 этого параграфа следует, что общие декартовы координаты точки М равны координатам ее радиуса – вектора 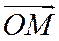, где О – начало координат.

Замечание 2. Утверждение теорем 3 и 4 может быть принято и за определение координат вектора.

Дата добавления: 2014-01-07