Выражение скалярного произведения в координатах

Ортонормированным базисом называется упорядоченная тройка 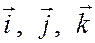единичных и попарно ортогональных векторов.

Пусть относительно ортонормированного базиса заданы два вектора своими координатами:

; ,

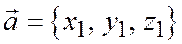то есть ; .

На основании свойств 1) – 3) скалярного произведения; находим

Но так как 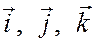- единичные попарно ортогональные векторы, то

; ,

значит .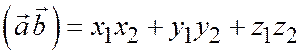

То есть скалярное произведение двух векторов, заданных своими координатами в ортонормированном базисе, равно сумме произведений их соответствующих координат.

В частности

,

где 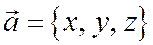, т.е. модуль вектора равен корню квадратному из суммы квадратов его координат, взятых относительно ортонормированного базиса.

Теперь из формулы находим косинус угла между двумя ненулевыми векторами, заданными своими координатами

;

относительно ортонормированного базиса; именно

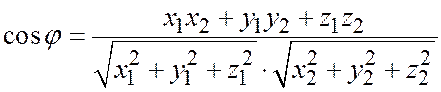. (3)

Из этой формулы находим необходимое и достаточное условие перпендикулярности двух ненулевых векторов:

. (4)

т.е. необходимым и достаточным условием ортогональности двух ненулевых векторов является равенство нулю суммы произведений соответствующих координат, взятых относительно ортонормированного базиса.

Теорема. Координаты x, y, z вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на единичные векторы базиса, т.е. .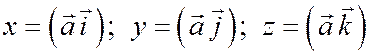

Доказательство: на основании теоремы 4 § 37 имеем

.

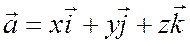(теорема 4: коэффициенты в разложении вектора 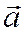по масштабным векторам 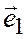, , 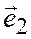общей декартовой системы координат в пространстве являются координатами вектора ).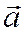

Продолжим доказательство теоремы.

Умножая скалярно обе части этого равенства поочередно на 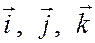в силу свойств скалярного произведения и соотношений

;

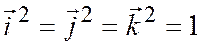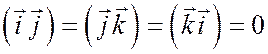
получим:

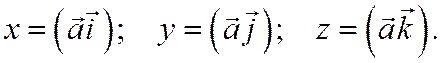
В частности, если вектор 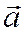единичный, то

,

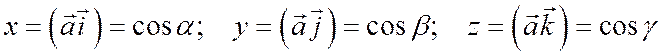где 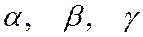- углы между вектором 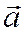и векторами .

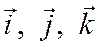Так как вектор 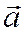единичный, то

,

а в силу формулы 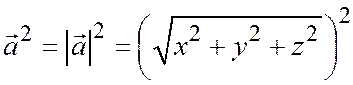имеем

.

Таким образом .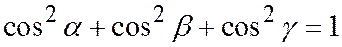

Косинусы углов вектора 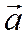с векторами 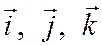ортонормированного базиса называются направляющими косинусами вектора или направляющими косинусами оси, имеющей направление вектора .

Мы видим, что сумма квадратов направляющих косинусов оси равна 1.

Если вектор не единичный, то из соотношений 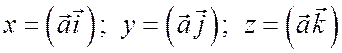находим и, так как , то

Задачи по Клетенику №№ 795-820.

Дата добавления: 2014-01-07