Для несвободной механической системы

ПРИНЦИП ГЕРМАНА - ЭЙЛЕРА - ДАЛАМБЕРА

При изучении движения несвободной механической системы, так же как и при изучении движения одной несвободной точки, применяют принцип освобождаемости от связей (см. § 21). По этому принципу имеющиеся связи отбрасывают, заменяя их действие соответствующими реакциями. Полученную механическую систему рассматривают как свободную, находящуюся под действием задаваемых сил и реакций связей.

Рассмотрим несвободную механическую систему, состоящую из n материальных точек. Применим к каждой точке М_i этой системы принцип Германа - Эйлера - Даламбера (см. § 106). Тогда 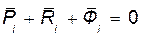(i=1, 2,..., n), (108.1)

где - равнодействующая задаваемых сил, приложенных к точке M_i. - равнодействующая реакций связей, приложенных к этой точке. - сила инерции материальной точки М_i.

Уравнение (108.1) показывает, что в любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакции связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.

Это положение называется принципом Германа-Эйлера-Даламбера для несвободной механической системы.

Сложим все n уравнений (108.1): 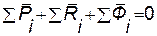(108.2)

Здесь - главный вектор задаваемых сил;

- главный вектор реакций связей;

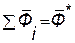- главный вектор сил инерции точек системы.

Подставляем эти значения в уравнение (108.2): 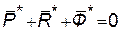(108.3)

Из уравнения (108.3) следует, что в любой момент времени для всякой несвободной механической системы геометрическая сумма главных векторов задаваемых сил, реакций связей и сил инерции материальных точек системы равна нулю.

Проведем из произвольного неподвижного центра О в каждую точку системы М_i радиусы-векторы 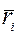. Умножим векторно радиус-вектор 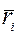каждой точки M_i на сумму векторов левой части равенства (108.1): 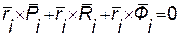(i=1,2,…,n) (108.4)↓

Сложим все n полученных уравнений:

Здесь 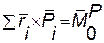- главный момент задаваемых сил относительно центра О;

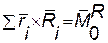- главный момент реакций связей относительно центра О;

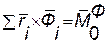- главный момент сил инерции точек системы относительно центра О. Подставляя эти значения в уравнение (108.4), получаем

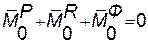(108.5)

Уравнение (108.5) показывает, что в любой момент времени для всякой несвободной механической системы геометрическая сумма главных моментов задаваемых сил, реакций связей и сил инерции материальных точек системы относительно любого неподвижного центра равна нулю.

Дата добавления: 2014-01-07