Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количеств движения всех материальных точек этой системы

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

Если отдельная точка системы M_k имеет массу 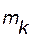и скорость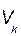, то вектор количества движения системы равен: 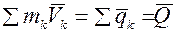(50.1)

Преобразуем выражение (50.1)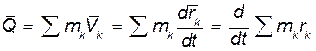

Так как согласно (32.1) 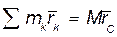, где 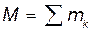- масса всей системы. То 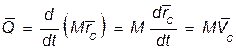и (50.2)

Выражение (50.2) показывает, что вектор количества движения механической системы имеет модуль, равный произведению массы всей системы на скорость ее центра масс и направление этой скорости.

Проектируем вектор 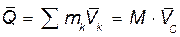на оси координат:

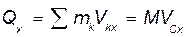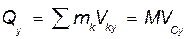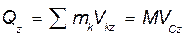, , (50.3)

Проекция количества движения механической системы на каждую координатную ось, равная сумме проекций количеств движения всех точек системы на эту ось, определяется произведением массы системы на проекцию скорости центра масс на эту же ось.

Дифференцируем (50.2) по времени: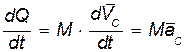

Согласно уравнению (43.1) движения центра масс системы ,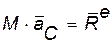

где 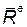- главный вектор внешних сил, действующих на систему материальных точек.

Следовательно, 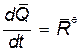(50.4)

Уравнение (50.4) выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему.

Векторному уравнению (50.4) соответствуют три уравнения в проекциях на оси координат:

(50.5)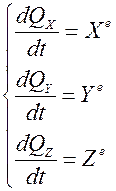где 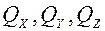проекции вектора количества движения 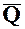на оси координат. 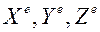проекции главного вектора внешних сил 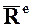на оси координат.

Уравнения (50.5) показывают, что производная по времени от проекции количества движения механической системы на любую ось равна проекции главного вектора внешних сил, действующих на систему, на ту же ось.

Из уравнений (50.4) или (50.5) следует, что изменение количества движения механической системы вызывается только внешними силами.

Закон сохранения количества движения механической системы:

Закон состоит из двух следствий из теоремы:

Следствие 1:

Дата добавления: 2014-01-07