Элементарная работа. Работа силы на конечном пути. Теоремы о работе силы. Изображение работы в виде площади

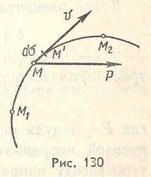
Предположим, что точка приложения переменной по модулю и направлению силы(Р) перемещается по криволинейной траектории из М₁ в М₂ (рис. 130).

Чтобы вычислить работу силы (Р) на этом перемещении, нужно разбить это перемещение на элементарные участки, вычислить работу силы на каждом элементарном участке как работу постоянной силы и определить предел суммы элементарных работ при стремлении числа участков к бесконечности и длины каждого из них к нулю. Элементарная работа силы (Р) на участке ММ' определяется по формуле (59.1):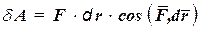 (60.1)

Здесь 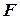(P)- модуль силы, соответствующей точке М; dr(dσ) — длина пути ММ', т. е. пройденный точкой элементарный путь; 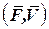- угол, составленный направлением силы 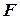(P) и скоростью 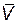в точке М.

Элементарную работу обозначают 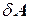а не dA, так как в общем случае она не является дифференциалом функции. Знак работы в выражении (60.1) определяется только знаком косинуса угла 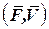. Будем определять положение точки М на траектории дуговой координатой s = 0M (рис. 131 и 132), а орт τ, направленный по касательной к траектории, направим в сторону возрастания дуговой координаты S (см. ч. I, «Кинематика» § 67 и 73).

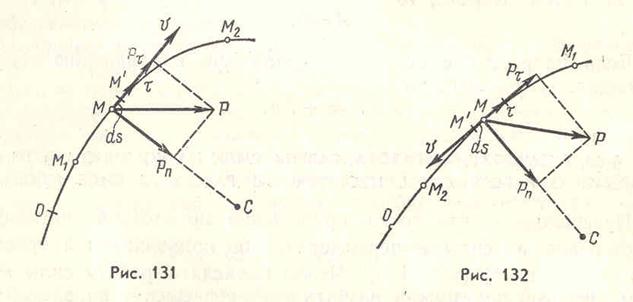
Тогда при движении точки М в сторону возрастания S (рис. 131) имеем:

1) dS>0,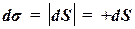

2) 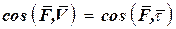, так как направления 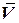и 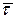совпадают.
Элементарная работа силы : .

При движении точки М в сторону уменьшения s (рис. 132) имеем:

1) dS<0;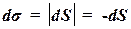

2)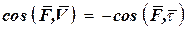, так как направления 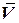и 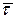противоположны.

Тогда элементарная работа силы :

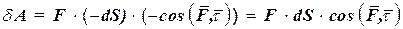
Таким образом, при движении точки в любом направлении по траектории элементарная работа силы: (60.2)

где F — модуль силы, соответствующей точке М; dS — приращение дуговой координаты точки (алгебраическая величина); 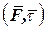- угол между направлением силы и орта τ, направленного всегда по касательной в сторону увеличения дуговой координаты.

В выражении (60.2) знак работы определяется как знаком dS, так и знаком синуса угла 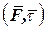. Обычно работа силы вычисляется отдельно для участков с движением в одном направлении. Тогда это направление принимается за положительное и в формуле (60.2) dS обозначает элементарный путь dσ, а угол 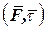является углом 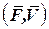(рис. 131).

Разложим силу на составляющие, направленные по касательной и главной нормали к траектории в точке М.

Проекции силы на касательную и главную нормаль определяются

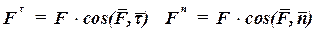. (60.3)

Пользуясь первой формулой(60.3), выражению (60.2) можно придать вид 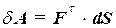(60.4)

Формула (60.4) показывает, что работу на перемещении dS совершает только касательная составляющая силы 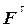, работа же нормальной составляющей 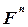, перпендикулярной к направлению скорости точки 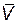, равна нулю. Согласно (59.2) представим элементарную работу силы (рис. 133) как скалярное произведение: 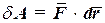(60.5)

где 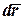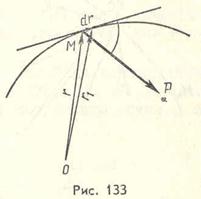- вектор элементарного перемещения точки М. о

Обозначив проекции силы на координатные оси X, Y, Z, а проекции вектора элементарного перемещения 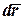на оси dх, dy, dz, получим скалярное произведение векторов и 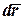в виде

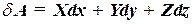. (60.6)

Формула (60.6) дает выражение элементарной работы через проекции силы на оси координат. Работа силы на конечном перемещении равна сумме ее работ на элементарных участках 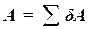. Пользуясь выражениями элементарной работы (60.1), (60.2), (60.4), (60.5) или (60.6) и переходя к пределу при стремлении числа участков к бесконечности, получаем следующие выражения работы силы Р на конечном перемещении М₁М₂:

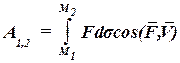(60.7)

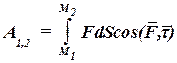(60.8)

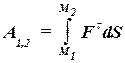(60.9)

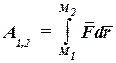(60.10)

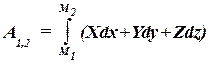(60.11)

Теоремы о работе силы. Теорема 1. Работа равнодействующей силы на некотором перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.

Предположим, что на точку М действуют силы 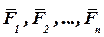(на рисунке Р₁, Р₂,..., Р_п) (рис. 134).

Равнодействующая этих сил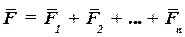

Если точка М получает элементарное перемещение 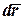, то элементарная работа равнодействующей силы на этом перемещении: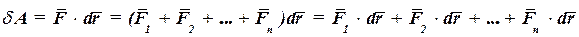

Для вычисления работы равнодействующей силы на конечном участке пути М₁М₂ воспользуемся формулой (60.10):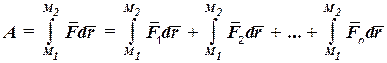

Полученная сумма криволинейных интегралов представляет собой сумму работ отдельных сил на конечном участке пути М₁М₂. Таким образом,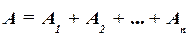

Теорема 2. Работа постоянной по модулю и направлению силы на результирующем перемещении равна алгебраической сумме работ этой силы на составляющих перемещениях.

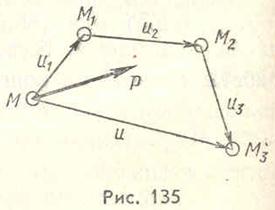
Предположим, что точка приложения постоянной по модулю и направлению силы получает совокупность последовательных перемещений 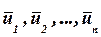(рис. 135, выполнен для n = 3).

Результирующее перемещение точки М: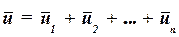

Работа силы на этом перемещении определяется по формуле (59.2) 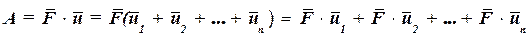Полученная сумма представляет собой сумму работ силы на составляющих перемещениях. Таким образом, 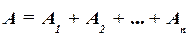На основании этой теоремы при вычислении работы постоянной силы на криволинейном перемещении криволинейное перемещение vможно заменить прямолинейным. При u = 0, т. е. в случае замкнутого контура, работа постоянной силы равна нулю.

Дата добавления: 2014-01-07