Работа силы упругости

Рассмотрим пружину АВ₁ конец А которой закреплен неподвижно (рис. 139, а).

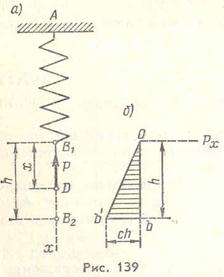При растяжении пружины в ней возникают силы упругости и на тело, вызывающее растяжение, действует реакция пружины Р. Эта сила направлена противоположно перемещению свободного конца пружины, а ее модуль пропорционален удлинению пружины ,

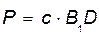где с — коэффициент жесткости пружины.

Направим ось Х по оси пружины, приняв за начало координат конец недеформированной пружины В₁. Проекция силы упругости на ось Х: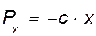

Вычислим работу силы упругости на перемещении при помощи формулы (60.6)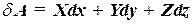

Проекции силы упругости, направленной по оси х, — на оси координат Х=-сх; Y= 0; Z = 0.

Элементарная работа силы упругости .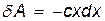

Работа силы упругости на перемещении B₁B₂ =h: (61.2)

Наибольшей деформации пружины B₁B₂ соответствует наибольшее значение силы упругости, а потому 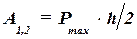(61.3)

Работа силы упругости отрицательна в том случае, когда деформация увеличивается, т. е. когда сила упругости направлена противоположно перемещению ее точки приложения, и положительна, когда деформация уменьшается.

Работа силы на перемещении B₂B₁ 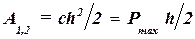(61.4)

На рис. 139, б показан график изменения проекции силы упругости 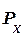в зависимости от перемещения конца пружины X. Так как , то линия графика Ob' — прямая.

Работа силы упругости определяется площадью треугольника Obb':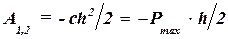

т. е. имеем тот же результат, который был получен аналитически.

Если начальная деформация пружины не равна нулю, а равна Хо, то работа силы упругости на дополнительной деформации (х₁ — х₀) равна:

(61.5)

Формулы (61.2) —(61.5) имеют большое применение в технических расчетах. Эти формулы используют для вычисления работы сил упругости во всех случаях, когда имеется пропорциональность между силами и деформацией, т. е. когда справедлив закон Гука.

Работа силы тяготения.

Допустим, что на материальную точку М массой т, расположенную в пространстве на расстоянии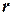от неподвижного притягивающего центра С массой т₀, действует сила тяготения:

Определим работу этой силы на перемещении точки из положения M₁ в положение М₂ (рис. 140). Проведем через неподвижный центр С оси декартовых координат.

Элементарную работу силы вычислим при помощи формулы (60.6):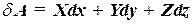

Здесь

Аналогично , .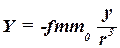

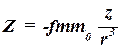Поэтому

Так как развёрнутый дифференциал проекций радиус-вектора можно чисто математически свернуть в дифференциал радиус-вектора в квадрате:

,

то

Работа силы тяготения Р при перемещении точки из М₁ в М₂ (61.6)

Как видно из (61.6), работа силы ньютонова притяжения не зависит от формы траектории точки.

Дата добавления: 2014-01-07