Теорема об изменении кинетической энергии механической системы

Установим зависимость между изменением кинетической энергии механической системы и работой приложенных к ее точкам сил. Для этого разделим силы, действующие на точки М₁, М₂, М₃,..., М_n, на внешние силы и внутренние силы . Применим к движению каждой точки M_i теорему об изменении кинетической энергии. Предположим, что при перемещении механической системы из первого положения во второе каждая точка M_i перемещается из М_i(1) в М_i(2), причем скорость ее изменяется от до (рис. 157).

Тогда по уравнению (62.3) для каждой материальной точки

где - работа силы и - работа силы на перемещении .

Просуммируем левые и правые части составленных n равенств

Согласно (67.1) 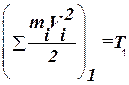- кинетическая энергия системы в первом ее положении; - кинетическая энергия системы во втором положении.

Таким образом, (69.1)

Уравнение (69.1) выражает теорему об изменении кинетической энергии механической системы: изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.

Согласно (65.4), сумма работ внутренних сил твердого тела на любом перемещении равна нулю, т. е.

Для твердого тела уравнение (69.1) принимает вид (69.2)

т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении.

Вопросы для самоконтроля:

19. Сформулируйте теорему Кенига о кинетической энергии механической системы в общем случае ее движения.

20. Как вычисляется кинетическая энергия твердого тела в различных случаях его движения?

21. Сформулируйте теорему об изменении кинетической энергии механической системы.

Дата добавления: 2014-01-07