Применение производных для вычисления пределов функций

(правило Лопиталя)

Вопросы отыскания пределов функций уже рассматривались выше. В данном параграфе речь пойдет об очень важном и практически удобном способе отыскания пределов отношений двух бесконечно малых или двух бесконечно больших функций при помощи производных. Этот способ называют правилом Лопиталя, т.к. оно впервые было опубликовано именно в книге французского математика Гильома де Лопиталя, хотя само открытие этого правила принадлежит Иоганну Бернулли.

Раскрытие неопределенностей вида и

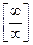
Теорема 6.5. (правило Лопиталя для неопределенности ). Пусть функции и 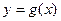непрерывны и дифференцируемы в окрестности точки и в самой этой точке равны нулю, т.е. 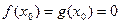. Если 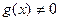в окрестности точки , тогда справедливо равенство

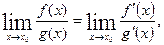(6.9)

если предел в правой части этого равенства существует.

Доказательство: применим теорему Коши для функций и 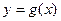и отрезка 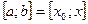, лежащего в окрестности точки . По этой теореме найдется такая точка 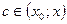, для которой выполнено равенство:

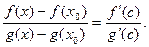
Но, по условию 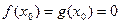, тогда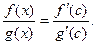

Пусть 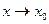, тогда величина 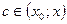также будет стремится к . Перейдем в последнем равенстве к пределу, получим:

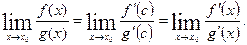Теорема доказана.

Следствие 1. Теорема верна и в том случае, когда 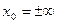. Действительно, положим 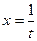, получим

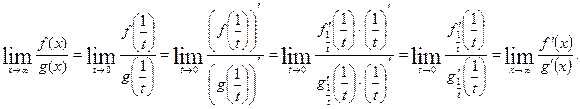
Следствие 2. Теорема верна и в том случае, когда функции и 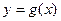не определены в точке , но существуют пределы и .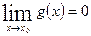

Пример 6.19. Пользуясь правилом Лопиталя, вычислить

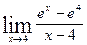
Решение.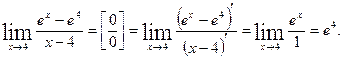

Замечание. При применении правила Лопиталя следует обратить внимание на то, что в правой части формулы (6.9) берется не производная отношения функции, а отношение производных двух функций.

Теорема 6.6. (правило Лопиталя для неопределенности 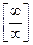). Пусть функции и 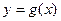непрерывны и дифференцируемы в окрестности точки , кроме, быть может, самой этой точки. Если 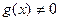в окрестности точки и 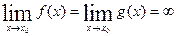, тогда справедливо равенство

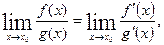(6.10)

если предел в правой части этого равенства существует.

Пример 6.21. Пользуясь правилом Лопиталя, вычислить

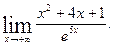
Решение.

В примере правило Лопиталя применено два раза.

Раскрытие неопределенностей вида , , ,,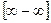

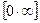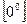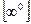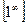
1. При раскрытии неопределенности вида 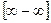, 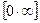следует сначала алгебраически преобразовать функцию, стоящую под знаком предела, для того чтобы получить неопределенности видаили 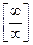, а затем применить правило Лопиталя.

Пример 6.22. Найти пределы а) 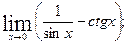б)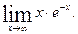

Решение. а) 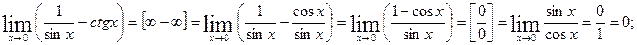б)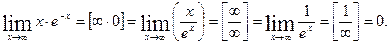

2. При раскрытии неопределенности вида 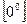,,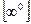 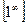вначале логарифмируют функцию, стоящую под знаком предела, затем по правилу Лопиталя находят предел ее логарифма.

Пример 6.23. Найти предел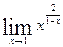

Решение. Имеет место неопределенность 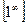. Вычислим предел логарифма данной функции

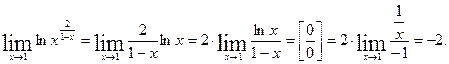
Итак, получ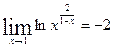или или 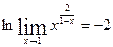, т.е.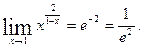

Правило Лопиталя удобное средство для нахождения пределов, однако не всегда решает поставленную задачу.

Пример 6.24. Найти предел .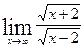

Решение.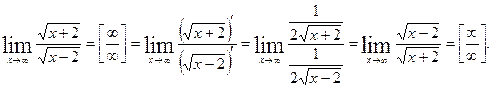

После применения правила Лопиталя, получили предел от функции, в котором числитель и знаменатель поменялись местами по сравнению с исходной функцией. Если правило Лопиталя применит еще раз, то можно опять вернуться к исходному пределу. Таким образом, для данного примера правило Лопиталя не позволило раскрыть неопределенность. Нетрудно понять, что такой предел можно найти без применения производных: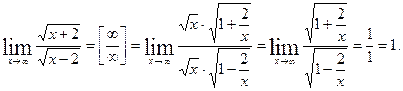

Дата добавления: 2014-01-07