Структурный синтез и анализ механизмов

Основные виды механизмов

Исходя из кинематических, конструктивных и функциональных свойств, механизмы подразделяют на:

1. Рычажные (рис. 2 а, б) - предназначенные для преобразования вращательного движения входного звена в возвратно-поступательное движение выходного звена. Могут передавать большие усилия и мощности.

2. Кулачковые (рис.2 в, г) - предназначенные для преобразования вращательного или возвратно-поступательного движения входного звена в возвратно-поступательное или возвратно-вращательное движение выходного звена. Придавая профилям кулачка и толкателя соответствующие очертания всегда можно осуществить любой желательный закон движения толкателя.

3. Зубчатые (рис. 2 е) - образованные с помощью зубчатых колес. Служат для передачи вращения между неподвижными и подвижными осями. Зубчатые передачи с параллельными осями осуществляются при помощи цилиндрических зубчатых колес, с пересекающимися осями - при помощи конических зубчатых колес, а со скрещивающимися осями - при помощи червяка и червячного колеса.

4. Фрикционные (рис. 2 д) - движение от ведущего звена к ведомому передается за счет сил трения, возникающих в результате контакта этих звеньев.

Структурным синтезом механизма называется проектирование структурной схемы механизма, которая состоит из неподвижного и подвижных звеньев и кинематических пар. Он является начальной стадией составления схемы механизма, удовлетворяющего заданным условиям. Исходными данными обычно являются виды движения ведущего и рабочего звеньев механизма, взаимное расположение осей вращения и направления поступательного движения звеньев, их угловые и линейные перемещения, скорости и ускорения. Наиболее удобным методом нахождения структурной схемы является метод присоединения структурных групп Ассура к ведущему звену или основному механизму.

Рис. 2.

Под структурным анализом механизма понимается определение количества звеньев и кинематических пар, определение степени подвижности механизма, а также установление класса и порядка механизма.

Степень подвижности пространственного механизма определяется по формуле Сомова - Малышева:

W = 6n-(5P₁+4P₂ + 3P₃ + 2P₄ + P₅) (1)

где Р₁ , Р₂, Р₃ , Р₄ , P₅ - число одно-, двух-,трех-, четырех- и пятиподвижных кинематических пар; n - число подвижных звеньев.

Степень подвижности плоского механизма определяется по формуле Чебышева:

W=3n-2P_H - P_B (2)

где рн - число низших, а Р_в- число высших кинематических пар.

В качестве примера рассмотрим четырехзвенный механизм рулевого управления автопилота (рис. 3.3): звенья 1 и 2 образуют цилиндрическую пару четвертого класса, имеющую две степени свободы; звенья 2-3 и 4-1 образуют вращательные пары пятого класса, имеющие одну степень свободы; звенья 3-4 образуют шаровую пару третьего класса, имеющую три степени свободы; число подвижных звеньев равно трем, тогда

W = 6 3-2 5-1 4-1 3 = 1

Степень подвижности данного механизма равна 1.

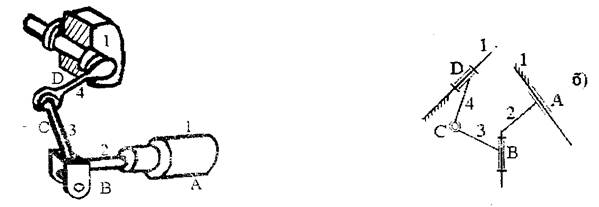
Рис. 3

Кинематическая цепь, число степеней свободы которой относительно элементов ее внешних кинематических пар равно нулю, называют структурной группой Ассура, по имени Л.В. Ассура, который впервые фундаментально исследовал и предложил структурную классификацию плоских стержневых механизмов. Пример образования плоского шестизвенного механизма дан на рис. 4.

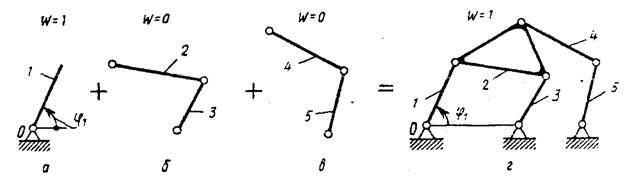
Рис. 4

Структурные группы подразделяют по классу и порядку. Класс группы определяется максимальным числом кинематических пар входящих в одно звено (рис. 5).

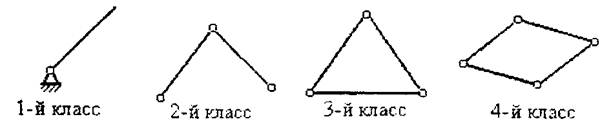
Рис. 5

Порядок группы определяется числом элементов, которыми группа присоединяется к основному механизму (рис. 6).

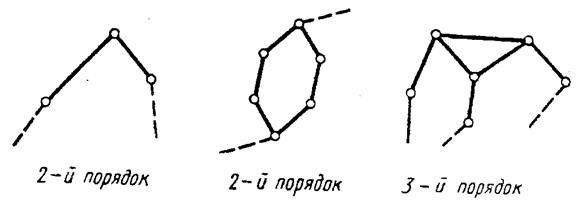
Рис. 6

Класс и порядок механизма зависят от того, какое звено является ведущим.

Дата добавления: 2014-01-07