Уравновешивание вращающихся звеньев

Лекция 13.

Тема №7. Колебания и уравновешивание механизмов

Решение задачи об уравновешивании динамических нагрузок в кинематических парах механизмов от сил инерции звеньев в общем виде представляет весьма большие практические трудности. Решение этой задачи заключается в таком распределении масс звеньев, при котором полностью или частично устраняются динамические нагрузки. При этом подборе масс конфигурации звеньев и их вес в большинстве случаев получаются мало конструктивными, а потому такой способ применяется главным образом при уравновешивании вращающихся деталей, обладающих значительной массой и большими угловыми скоростями. Сюда надо отнести валы быстроходных двигателей, барабаны центрифуг, турбины, тарелки сепараторов, барабаны молотилок, якори динамомашин, веретена, роторы гироскопов и т. д. Частота вращения некоторых из этих деталей достигает 20000...50000 об/мин и более. При этих условиях работы чрезвычайно важным является вопрос о правильном распределении масс этих деталей относительно их оси вращения.

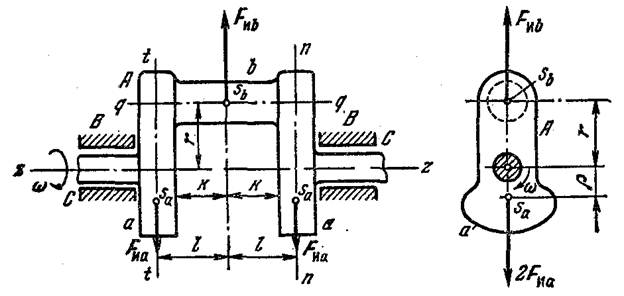
Рис. 1. Коленчатый вал двигателя

Пусть, например, мы имеем коленчатый вал А (рис. 1), вращающийся вокруг неподвижной оси z — z с угловой скоростью ω. Чтобы подшипники В не испытывали дополнительных динамических давлений от сил инерции масс вала, необходимым и достаточным является условие равенства нулю главного вектора сил инерции масс материальных точек вала. Как известно из теоретической механики, это условие всегда удовлетворяется, если центр масс вращающегося звена лежит на его оси вращения, которая должна быть одной из его главных осей инерции. Если конструктивное оформление вала (рис. 1) удовлетворяет этому условию, то вал получается уравновешенным, что при проектировании достигается соответствующим выбором формы уравновешиваемой детали. Например, коленчатый вал (рис. 1) имеет фигурные щеки а, коренные шейки С и шатунную шейку b. Рассматривая в отдельности эти элементы вала, мы видим, что центр масс материальных точек коренных шеек располагается на оси вращения z— z вала. Центр масс S_b точек шатунной шейки b находится на ее геометрической оси q — q на равных расстояниях от щек а. Центробежная сила инерции F _{и b} шейки b равна по величине

(1)

где т_b — общая масса шатунной шейки.

Сила инерции F _{и b} может быть полностью уравновешена соответствующим подбором масс m_a щек и их центров масс S_a (рис. 1). Для этого центры масс S_a должны лежать в плоскостях t — t и п — п, симметрично расположенных относительно точки S_b на расстоянии ρ от оси z — z вала так, чтобы удовлетворялось условие

(2)

В самом деле, если помножить правую и левую части равенства на ω², то получим

или, согласно формуле (1),

Таким образом, суммарная сила инерции 2F _{и а} щек а полностью уравновешивает силу инерции F _{и b} шатунной шейки. Из уравнения моментов всех сил инерции относительно точки S_b следует, что момент от всех сил инерции масс вала также равен нулю. Таким образом, мы имеем равенство нулю как главного вектора сил инерции, так и главного вектора момента от сил инерции вала, т. е. этот вал полностью уравновешен.

При этом, динамические нагрузки от сил инерции масс звеньев будут равны нулю и при вращении вала с угловым ускорением ε.

Рассмотрим более общий случай уравновешивания вращающегося звена, когда с валом, вращающимся в подшипниках А, жестко связаны заданные массы m₁, m₂ и m₃ (рис. 2, а). Пусть центры масс m₁, m₂ и m₃ расположены в трех плоскостях Т₁, Т₂ и Т₃, перпендикулярных к оси вращения z—z, на расстояниях ρ₁ ρ₂ и ρ₃. Величины центробежных сил инерции, развиваемых этими массами, равны

Переносим все эти силы в какую-либо плоскость Т₀, проведенную через произвольную точку О вала, перпендикулярно к оси z—z. Для этого в точке О каждый раз прикладываем по две равные, но противоположно направленные силы, величины которых равны F _иl, F _и2 и F _и3 . Далее складываем все перенесенные силы, для чего строим силовой многоугольник (рис. 2, б). Так Как величины сил F _иl, F _и2 и F _и3 пропорциональны произведениям масс т на соответствующие расстояния ρ, то вместо сил F _иl, F _и2 и F _и3 можно откладывать в силовом многоугольнике произведения m₁p₁ , m₂p₂ и m₃p₃ являющиеся статическими моментами масс относительно оси вращения. Вектор m р определяет величину уравновешивающей силы F_y

(3)

Уравновешивающая масса т может быть установлена в любой точке по длине вала и на любом расстоянии р от его оси вращения,

Рис. 2.

К уравновешиванию нескольких масс, жесткоустановлевных на валу отложенном в направлении вектора тр (рис. 2, а). Необходимо только, чтобы произведение тр удовлетворяло плану сил, построенному на рис. 2, б. В рассматриваемом примере центр массы т расположен в плоскости Т.

Установкой противовеса, удовлетворяющего формуле (3), уравновешиваются статические нагрузки на подшипники А от результирующей силы инерции. Для уравновешивания динамических нагрузок от моментов сил инерции находим моменты М_и1, М_и2 и М_и3 этих сил относительно точки О. Имеем

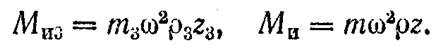(4)

Строим многоугольник моментов (рис. 2, в). Так как плоскости действия всех пар содержат ось z—z, то многоугольник моментов лежит в плоскости, перпендикулярной к оси z—z. Направление векторов моментов выбираем так, чтобы, смотря вдоль по вектору, видеть вращение происходящим против часовой стрелки. Так как величина ω² в равенствах (4) входит в виде

постоянного множителя, то величину вектора результирующего момента можно подсчитать, не вводя этого множителя.

Замыкающий вектор m₀p₀Z₀ в многоугольнике моментов (рис. 2, в) определит величину момента и плоскости действия уравновешивающей пары. Обозначим этот момент через М _и0. Имеем тогда

(5)

Плоскость действия уравновешивающей пары вполне определится замыкающим вектором .Она перпендикулярна к этому вектору и содержит ось z — z. Уравновешивающие массы m₀ могут быть в этой плоскости установлены в любых точках вала. В качестве плоскостей установки уравновешивающих грузов с массой m₀ по оси z —z выбираем те же плоскости Т₀ и Т. Тогда при заданном расстоянии z₀ между этими плоскостями необходимо подобрать такие значения масс m₀ и расстояний р₀ их центров масс от оси z—z, чтобы удовлетворялось равенство (5). Одна из этих масс устанавливается так, чтобы ее центр масс находился в плоскости Т ₀; другая масса устанавливается так, чтобы ее центр масс находился в плоскости Т. Знак момента этой пары определяется замыкающим вектором многоугольника моментов (рис. 2, б).

Таким образом, установкой двух противовесов массы m₀ и одного противовеса массы m достигается полное уравновешивание всех масс, закрепленных на валу. Так как один из противовесов массы m₀ расположен в той же плоскости Т (рис. 2, а), что и противовес массы т, то массы m₀ и m можно заменить одной массой. Следовательно, полное уравновешивание масс, закрепленных на валу, может быть достигнуто установкой двух противовесов, центры масс которых лежат в двух произвольно выбранных плоскостях.

Правильно спроектированная с точки зрения полного уравновешивания деталь все же может иметь некоторую неуравновешенность вследствие неоднородности материала, из которого она изготовлена, неточности обработки и т. д. Поэтому все быстро вращающиеся детали проверяют опытно на специальных машинах, которые называются балансировочными машинами. Конструкции балансировочных машин очень разнообразны, но большинство из них основано на принципе установки испытуемой детали на упругое основание (люлька на пружинах, подшипники на упругом основании и т. д.) и сообщения этой детали скорости, близкой к резонансной. Тогда неуравновешенные силы создают значительные амплитуды колебаний, которые регистрируются специальными устройствами, позволяющими определить места, в которых надо установить уравновешивающие массы или удалить лишнее количество материала.

Рассмотрим процесс динамической балансировки на станке Б. В. Шитикова, схема которого показана на рис. 3. Балансируемая деталь 1, представляющая собой в рассматриваемом случае ротор с фланцем В, укладывается в подшипники люльки 2, которая свободно вращается вокруг оси О— О. Второй конец люльки в точке А скреплен о пружиной 5, имеющей регулировку, позволяющую устанавливать вал z — z горизонтально. Амплитуды колебаний люльки вокруг оси О— О записываются индикатором D.

Рис. 3. Схема балансировочного станка Шитикова.

Как было показано выше, все центробежные силы отдельных частиц вращающегося тела могут быть сведены к эквивалентной системе двух сил F _и1 и F _и2 , лежащих в двух произвольно выбранных плоскостях I и II (рис. 4). В рассматриваемом примере плоскость I проходит через среднее сечение фланца (рис. 3).

Рис. 4. Схема балансируемого ротора

Эти силы могут быть представлены как центробежные силы, возникающие от двух точечных масс m₁ и m₂, расположенных в плоскостях I и II на расстояниях р₁ и р₂ от оси вращения. Силы F _и1 и F _и2 равны по величине

Как было показано выше, угловая скорость ω² входит в выражения для сил постоянным множителем. Поэтому величины сил F _и1 и F _и2 можно характеризовать статическими моментами масс m₁p₁ и m₂p₂.

Если в плоскостях I и II установить массы m_I и m_II на расстояниях r _I и r _II, так чтобы удовлетворялись условия

(6)

и

(7)

то силы инерции ротора будут полностью уравновешены.

Если вывести раму с ротором из равновесия (например, надавить на один из подшипников, а потом отпустить его), то рама придет в колебательное движение, которое вследствие сопротивления воздуха и трения в оси О — О будет затухающим и прекратится.

Частота k этого колебания является постоянным параметром для данной установки; она зависит от момента инерции колеблющейся системы относительно оси О-О, жесткости пружины и в малой степени от сопротивления среды и называется частотой собственных (свободных) колебаний системы.

Установим ротор в подшипниках так, чтобы плоскость II (она, вообще говоря, может быть выбрана произвольно) проходила через ось вращения О — О. Приведем ротор в быстрое вращение. Вертикальная слагающая центробежной силы F _и1, равная F _и1 cos ωt ( рис. 5), создает вокруг оси О—О момент М_и1 = F _и1 z₀ cos ωt. Сила F ₂ располагается в одной плоскости II с осью О — О, и потому момент ее вокруг этой оси равен нулю.

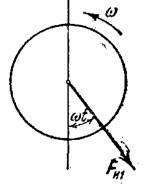
Рис. 5.

Вектор центробежной силы неуравновешенной массы ротора

Момент М_и1, изменяющийся по гармоническому закону с частотой ω, равной угловой скорости ротора, вызывает вынужденные незатухающие колебания люльки. По мере убывания угловой скорости со ротора уменьшается и частота изменения возмущающего момента М_и1. Когда эта частота станет близкой к собственной частоте колебаний системы k, возникает состояние резонанса; в это время амплитуда колебаний люльки станет наибольшей. Из теории колебаний известно, что при резонансе амплитуда А вынужденных колебаний может считаться пропорциональной амплитуде возмущающего фактора:

(8)

где μ — коэффициент пропорциональности, зависящий от постоянных параметров данной установки.

Если определить постоянную μ данного станка, то по амплитуде А, зафиксированной на индикаторе D, можно установить величину силы F_и1, определяющей дисбаланс, отнесенный к плоскости I, Это дает возможность определить искомое значение m_Ir_I.

Таким же образом, повторив испытание, но установив ротор плоскостью I на место плоскости II, можно определить и значение m_IIr_II.

Однако остался нерешенным еще вопрос о линии действия сил F _и1 и F _и2 , т. е. об отыскании тех направлений в плоскостях

I и II, на которых нужно укрепить противовесы с точечными массами m_I и m_II.

Для определения коэффициента пропорциональности μ и направлений, в которых необходимо установить массы m_I и m_II, можно воспользоваться приемом, который сводится к тому, что к балансируемой детали искусственно присоединяется дополнительная масса m_д на некотором расстоянии р_д от оси вращения детали. Обычно в качестве такой массы берут кусок пластилина массы m_д, и этот кусок прикрепляют к поверхности балансируемой детали. На рис. 3 куски этой массы показаны на поверхности фланца В. Масса m_д носит название корректирующей массы.

Рис. 6.

К определению положения корректирующей массы при уравновешивании ротора:

а) положение вектора центробежной силы при первом испытании;

б) векторная диаграмма действующих сил после установки корректирующей массы;

в) векторная диаграмма действующих сил при третьем испытании о корректирующей массой.

Рис. 7. Диаграмма для определения статического момента противовеса, уравновешивающего ротор.

Разгоняем ротор до быстрого вращения, после чего отключаем приводное устройство, переводим ротор в режим выбега и измеряем величину максимальной амплитуды на индикаторе D. Пусть эта амплитуда равна А₁ (мм).

Устанавливаем корректирующую массу m_д (рис. 3) в плоскости I на расстоянии р_д от оси z—z, равном внешнему радиусу фланца, приводим во вращение ротор и снова замеряем на индикаторе наибольшую амплитуду. Пусть эта амплитуда равна A₂. Наконец, устанавливаем корректирующую массу m_д на том же расстоянии р_д от центра фланца В, но по другую сторону от него, и приводим во вращение ротор и снова замеряем наибольшую амплитуду. Пусть эта амплитуда равна А₃. По полученным амплитудам A₁, A₂ и A₃ можно определить величину m_Ir_I (см. формулу (8)). На рис. 6, а показана сила F_sl, вызывающая вынужденные колебания в первом испытании.

На рис. 6, б показана сила F' _и, полученная вследствие установки корректирующей массы m_и при втором испытании. Имеем

На рис. 6, в показана сила Р" _и , полученная вследствие установки корректирующей массы при третьем испытании. Имеем

как как

Совместим заштрихованные на рис. 6, б и в треугольники так, чтобы равные их стороны а совпадали (рис. 7). Тогда получаем параллелограмм BCDE, у которого стороны а, b, с и d и диагонали связаны условием

или

(9)

Так как, согласно равенству (13.64), А ₁ — μF _и1, А₂ = μF' _и А ₃ = μF'' _и и A _д = μF' _и2 = μF'' _и2 , где μ — общий коэффициент пропорциональности, зависящий от параметров установки, то, заменяя в равенстве (9) отрезки с, d, BD и СЕ их значениями, равными

получаем

Так как амплитуды А ₁ , A ₂ и А ₃ нами могут быть измерены, то из формулы (8) можно определить амплитуду A_д. Согласно условию (8)

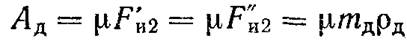
Из последнего равенства определяем коэффициент пропорциональности μ.:

Величина статического момента т _I r _II уравновешивающего противовеса может быть теперь получена из формулы:

Угол а (рис. 6, а) между направлением, на котором надо установить противовес т _I, и направлением установки корректирующей массы m_д определяется, согласно рис. 7, из соотношения

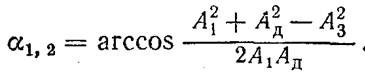(12)

Из последнего соотношения будут получены два значения угла а. Вопрос о пригодности того или другого значения решается испытанием на станке: противовес m_I на выбранном расстоянии r_I устанавливается сначала под углом a ₁, а затем под углом a ₂; пригодной является та установка, при которой вибрации отсутствуют (даже при критической, т. е. резонансной угловой скорости).

Поменяв местами плоскости I и II, т. е. установив ротор на станке так, чтобы его ось была повернута на 180° относительно первоначального положения, мы тем же способом можем найти статический момент m_IIr_II уравновешивающего противовеса m_II устанавливаемого в плоскости II. Практически устранение неуравновешенности производится или удалением части массы детали, или закреплением дополнительной массы.

Таким образом, установив в плоскостях I и II противовесы m_I и m_II, мы полностью уравновешиваем силы инерции ротора.

Дата добавления: 2014-01-07