Вибрационные машины и принцип их действия

Лекция 14.

Тема №7. Колебания и уравновешивание механизмов

Вина региона Валле д’Аоста

Долина Aosta, горный район, расположена на северо-западе Италии. В ней живет около 118 тыс. человек. Приобрела мировую известность за расположенные на ее териитории высокие горы: Mont Blanc, Matterhorn, Gran Paradiso и Monte Rosa, красивое место, где есть возможность заниматься разнообразными зимними видами спорта.
Фуникулеры и подъемники могут поднять вас на высоту более 3000 метров. Весьма интересные для катания на лыжах трассы и склоны зимой и для горных прогулок летом. Захватывающие дух виды вокруг.
Земледелие все еще имеет большое значение для местного населения. Особо интересно виноделие.
Оно специализировано на выращивании винограда на скалах, но тяжелая работа вознаграждается небольшим количеством великолепных, редких и незабываемых вин. Виноградники здесь самые высотные в Европе!
Другие типичные деликатесы: сыр Fontina, сосиски, мясо серны,...
Автономный регион субсидирует сельское хозяйство, с акцентом на качество.
30-го и 31-го января долина Аоста собирает посетителей (уже тысячу лет) из прилежащих регионов и из-за границы на ежегодную ярмарку ремесел "St Orso", где представлены традиционные деревянные и железные произведения исскуства. Позже ярмарка стала проиводится и летом, в субботу, предшесвтвущую выходным в середине августа.
Aosta, в древности Augusta Praetoria, основанная римлянами, является местом где встречаются исскуство и культура. Благодаря историческим памяниткам и руинам Древнего Рима и Средних Веков.
В Аосте, столице с ее административными офисами, мы можем найти только "большие" фабрики, производящие сталь. Другие, более мелкие фабрики находятся в Шатильоне: "tecdis" производит мониторы, на горе S. Martin, находится фабрика преобразоватлей. Конгресс-центр в Saint Vincent с его казино предоставляет сотням людей хорошую жизнь. Но долина Аосты не только индустриальное место, она прежде всего прекрасное место отдыха.
В Aosta Valley есть два официальных языка: французский и итальянский. Французский изучается уже в детском саду. Местные население говорит на "Patois", происходящем от "Franco-Provencal" языка.
Вы можете попасть в Aosta Valley через два туннеля, которые связывают ее с Францией и Италией.

Силы инерции не всегда являются вредными, с которыми надо бороться. В настоящее время имеется много машин, в которых для выполнения того или иного технологического процесса намеренно возбуждаются колебания. Машины, в которых технологический процесс выполняется на основе возбужденных колебаний, называют вибрационными машинами. Возбудителями колебаний в этих машинах могут быть механические и электромагнитные вибраторы, гидравлические и пневматические пульсаторы. Рабочему органу машины, взаимодействующему с обрабатываемой средой, необходимо придать колебательное движение с желаемой частотой колебаний и амплитудой.

Вибрационные машины получили большое распространение в различных отраслях промышленности и в сельском хозяйстве. С помощью вибраций дробят, измельчают, транспортируют кусковой и сыпучий материал, разделяют смеси, уплотняют бетон, погружают сваи и шпунт в грунт, просеивают различные продукты. Используют вибрации и в быту (например, вибрационные бритвы). Обрабатываемые среды под действием вибраций становятся более «податливыми», что способствует интенсификации технологического процесса.

Наиболее распространенным возбудителем колебаний является дебалансный возбудитель. Устройство простейшего дебалансного вибратора показано на рис. 1, а. Неуравновешенная масса m вращается около оси А с угловой скоростью со и развивает центробежную силу инерции F _и, равную F _и — mpω², где р — расстояние центра массы m от оси А, Сила инерции дебаланса через опору А передается массе М, с которой обычно и связывается рабочий орган вибромашины, взаимодействующий с обрабатываемой средой.

На рис. 1. б показан дебалансный вибратор направленного действия, в котором два дебаланса т вращаются с одинаковой скоростью в противоположных направлениях. Горизонтальные составляющие F _их двух центробежных сил инерции F' _и взаимно уравновешиваются, а вертикальные F _{и у} — складываются, образуя суммарную силу инерции

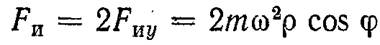
где φ — угол, образуемый силой F' _и с вертикальной осью. Часто

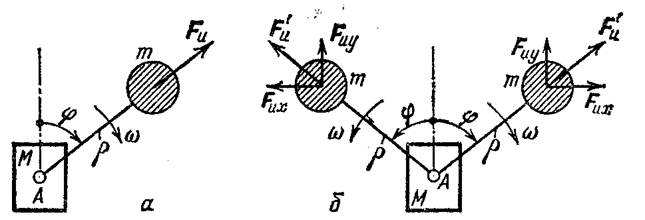
Рис. 1.

Схемы возбудителей колебаний механического типа:

а) схема простейшего дебалансного вибратора;

б) схема дебалансного вибратора направленного действия полагают, что дебалансы вращаются с постоянной угловой скоростью ω, тогда φ = ωt и сила F _и является периодической функцией времени:

т. е. в этом возбудителе колебаний возбуждающая сила по направлению всегда совпадает с осью углов, а по величине меняется по гармоническому закону. Дебалансы обычно имеют между собой кинематическую связь, а иногда такой связи нет, но при определенных условиях оба дебаланса все равно вращаются с одинаковыми скоростями; в таких случаях говорят о самосинхронизации дебалансов. Форма движения массы М определяется характером ее подвески к неподвижной части машины, физико-механическими свойствами среды и механической характеристикой двигателя, приводящего во вращение дебаланс m.

Общим для всех вибромашин является следующее: Во-первых, вибрационная машина является колебательной системой, состоящей из возбудителя колебаний — вибратора и колеблющейся массы, т. е. рабочего органа и частей, жестко с ним скрепленных. Во-вторых, рабочий процесс в вибромашинах получается в результате суммарного эффекта большого количества отдельных циклов, следующих один за другим. Хотя эффект за один цикл является незначительным, но высокая частота этих циклов делает эти машины высокоэффективными.

Динамическое исследование вибромашин состоит в составлении и решении уравнений движения. В уравнения движения входят:

1) возбуждающая сила вибратора,

2) восстанавливающие силы, зависящие от способа подвески рабочего органа,

3) силы взаимодействия вибрирующего органа со средой,

4) инерционные силы рабочего органа.

На рис. 2 изображена динамическая модель вибрационной машины. Дебалансный возбудитель направленного действия создает возбуждающую колебания силу F _и периодического действия, которая передается массе М, а с массой М связан исполнительный орган — или сито для просеивания или разделения материалов, или дека для вибротранспортирования материалов и т. д. Пружина с жесткостью с и демпфер с коэффициентом затухания b моделируют систему упругой подвески к неподвижному корпусу машины, взаимодействие с обрабатываемой средой и другие потери.

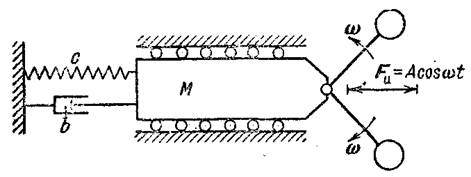
Рис. 2. Динамическая модель вибрационной машины с дебалансным вибратором направленного действия

Возьмем простейшую, так называемую линейную колебательную систему, в которой возбуждающая сила меняется по гармоническому закону

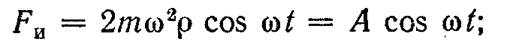
здесь

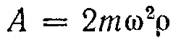
есть амплитудное значение возбуждающей силы.

Обозначим через х линейную координату перемещения массы М, тогда упругая сила пружины будет — сх, где с — жесткость пружины. Демпфирующие свойства системы представим тоже в виде линейной функции скорости — b^∙х.

Теперь, проектируя все силы, приложенные к массе М, на направление х, получим уравнение колебаний массы М

(1)

Часто это уравнение представляют в таком виде;

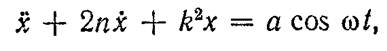(2)

где

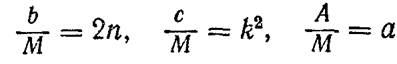
Если выписать полное решение этого линейного дифференциального уравнения второго порядка с правой частью, то получим закон движения массы М, в котором будут смешаны свободные колебания системы, зависящие от начальных условий и параметров системы, и вынужденные колебания, определяемые характером возбуждения и параметрами системы. Как показывает практика, свободные колебания в системе затухают довольно быстро и остаются лишь вынужденные колебания. Вибрационные машины основной технологический процесс выполняют в установившемся режиме, когда свободные колебания уже затухнут,

и на этот режим обычно проектируется машина. Решение вынужденных колебаний массы М имеет вид

(3)

где δ — сдвиг фаз изменения возбуждающей силы и перемещения массы М,

а— амплитуда колебаний массы М.

Интенсивность технологического процесса определяется, главным образом, амплитудой колебаний (точнее, размахом колебаний) и частотой возбуждающей силы. Под размахом А колебаний понимают удвоенную амплитуду колебаний при гармонических и других симметричных колебаниях, или разность между максимальными и минимальными отклонениями при несимметричных колебаниях.

Из уравнений (1), (2) и решения (3) можно видеть, что размах колебаний Δ зависит от пяти параметров:

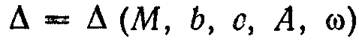
Рис. 10. Амплитудно-частотные характеристики вибрационной машины при различных коэффициентах затухания

Конструктор может варьировать этими параметрами, чтобы получить наиболее приемлемый технологический процесс вибромашины.

Следует заметить далее, что амплитуда колебаний Н существенно зависит от соотношения между k ² и ω². Зависимость Н от ω / k в колебательных системах называют амплитудно-частотной характеристикой; типичный вид характеристик показан на рис. 10, где они построены для различного затухания b.

Конечно, во многих случаях вибрационные машины явля ются более сложными, чем показано в этом параграфе; упругая сила подвески и демпфирующая сила — нелинейные, скорость вращения дебалансов не принимается постоянной, а учитывается характеристика двигателя, и подвеска часто обеспечивает движение массы не только прямолинейное, но и плоское или пространственное; в некоторых случаях приходится учитывать присоединяемую к М массу обрабатываемого продукта.

Дата добавления: 2014-01-07