
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П. 4.3. Формулы логики предикатов. Равносильные формулы
|
|
|
|
В логике предикатов пользуются следующей символикой:
1. Символы 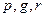 – переменные высказывания.
– переменные высказывания.
2. Предметные переменные – 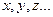 , которые пробегают значения из некоторого множества
, которые пробегают значения из некоторого множества  – предметные константы.
– предметные константы.
3.  – предикатные символы.
– предикатные символы.
4. Символы логических операций 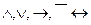 .
.
5. Символы кванторных операций 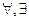 .
.
6. Вспомогательные символы: скобки, запятые.
Определение 4.12. Формулой логики предикатов называется всякое выражение, символику 1-6 и удовлетворяющее следующим требованиям:
1) Каждое высказывание как переменное, так и постоянное является формулой;
2) Если  – n - местная предикатная переменная или постоянный предикат, а
– n - местная предикатная переменная или постоянный предикат, а  – предметная переменная или постоянная, то
– предметная переменная или постоянная, то  – формула.
– формула.
3) Если А и В – формулы, то  ,
,  ,
,  – тоже формулы при условии, что одна и та же предметная переменная не является в А свободной, а в В – связанной или наоборот.
– тоже формулы при условии, что одна и та же предметная переменная не является в А свободной, а в В – связанной или наоборот.
4) Если А – формула, то  – тоже формула.
– тоже формула.
5) Если 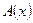 – формула, то
– формула, то  и
и 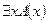 являются формулами, причем если в
являются формулами, причем если в 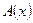 х – свободная переменная, то в
х – свободная переменная, то в  и
и 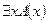 х будет уже связанной переменной.
х будет уже связанной переменной.
6) Всякое слово, отличное от тех, которые названы формулами в п.1-5 не является формулой.
Пример 12:
а)  не является формулой, так как квантор существования употреблен для уже связанной квантором всеобщности переменной у;
не является формулой, так как квантор существования употреблен для уже связанной квантором всеобщности переменной у;
б)  – формула, х – связанная переменная, у – свободная;
– формула, х – связанная переменная, у – свободная;
в) 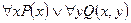 не является формулой, ибо в первом логическом слагаемом х – связанная переменная, а во втором слагаемом – свободная.
не является формулой, ибо в первом логическом слагаемом х – связанная переменная, а во втором слагаемом – свободная.
Логическое значение формулы логики предикатов зависит от значений трех видов переменных: значений переменных высказываний, входящих в формулу, значений свободных предметных переменных из множества М и значений предикатных переменных. Если фиксировать значения каждого из трех видов переменных, формула логики предикатов становится высказыванием, имеющим истинное или ложное значение.
Пример 13:
Даны предикаты 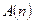 : "число n делится на 3",
: "число n делится на 3",  : "число n делится на 2",
: "число n делится на 2",  : "число n делится на 4",
: "число n делится на 4",  : "число n делится на 6",
: "число n делится на 6", 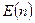 : "число n делится на 12". Указать, какие из следующих утверждений истинны, а какие ложны.
: "число n делится на 12". Указать, какие из следующих утверждений истинны, а какие ложны.
1. 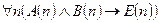 . Рассмотрим составляющие части этой формулы.
. Рассмотрим составляющие части этой формулы. 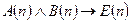 : "Если число n делится на 6, то оно делится на 12". При n = 6 импликация ложна, следовательно формула
: "Если число n делится на 6, то оно делится на 12". При n = 6 импликация ложна, следовательно формула 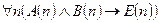 – ложна.
– ложна.
2. 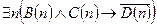 . Поступаем аналогично.
. Поступаем аналогично. 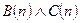 : "Число n делится на 4".
: "Число n делится на 4".  : "Если число n делится на 4, то оно не делится на 6". Существует n = 16, при котором эта формула принимает значение истинно, то есть формула
: "Если число n делится на 4, то оно не делится на 6". Существует n = 16, при котором эта формула принимает значение истинно, то есть формула  не является тождественно ложной, а тогда
не является тождественно ложной, а тогда 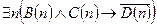 – истинная формула.
– истинная формула.
Истинность и ложность логики предикатов может быть проверена путем приписывания смысла языковыми конструкциями, то есть их интерпретация. Для того, чтобы определить интерпретацию, необходимо задать множество значений, которые могут принимать свободные переменные, отношения для предикатных символов.
Пример 14:
 – формула, содержащая свободную переменную у.
– формула, содержащая свободную переменную у.
а) Пусть  интерпретируется как "
интерпретируется как "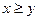 " на
" на  . Если
. Если  , то посылка в импликации истинна, а заключение ложно и формула ложна.
, то посылка в импликации истинна, а заключение ложно и формула ложна.
Если 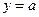 , то левая и правая части истинны и вся формула истинна, следовательно, формула выполнима в данной интерпретации.
, то левая и правая части истинны и вся формула истинна, следовательно, формула выполнима в данной интерпретации.
б) Если  интерпретируется как "
интерпретируется как "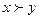 " на
" на  , то левая часть будет всегда истинной (при любом у), а правая – всегда ложна, следовательно, формула тождественно ложна в данной интерпретации.
, то левая часть будет всегда истинной (при любом у), а правая – всегда ложна, следовательно, формула тождественно ложна в данной интерпретации.
Определение 4.13. Две формулы логики предикатов А и В равносильны в данной интерпретации, если на любом наборе значений свободных переменных они принимают одинаковые значения, то есть формулы выражают в данной интерпретации один и тот же предикат.
Определение 4.14. Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех входящих в них переменных, отнесенных к области М.
Определение 4.15. Две формулы логики предикатов А и В равносильны, если они равносильны на всякой области 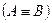 .
.
Все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний представить формулы алгебры предикатов. Но имеются равносильности самой логики предикатов, связанные с кванторами. Пусть 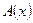 и
и 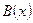 – переменные предикаты, а С – переменное высказывание. Тогда имеют место такие формулы:
– переменные предикаты, а С – переменное высказывание. Тогда имеют место такие формулы:
1. 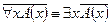 , читается: «высказывание "не верю, что для любого х
, читается: «высказывание "не верю, что для любого х 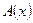 " эквивалентно высказыванию "найдется х, для которого не
" эквивалентно высказыванию "найдется х, для которого не 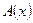 "».
"».
2. 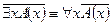 .
.
3. 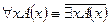 .
.
4.  .
.
5.  .
.
6.  .
.
7. 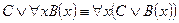 .
.
8. 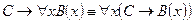 .
.
9.  .
.
10.  .
.
11.  .
.
12. 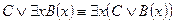 .
.
13. 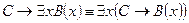 .
.
14. 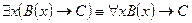 .
.
15.  .
.
16.  .
.
Докажем равносильность 5.
а) Если предикаты 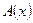 и
и 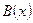 одновременно тождественно истинны, то будет истинным и предикат
одновременно тождественно истинны, то будет истинным и предикат  , высказывания
, высказывания  ,
, 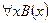 ,
, 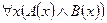 , то есть обе части принимают значение истины.
, то есть обе части принимают значение истины.
б) Если оба предиката будут тождественно ложными или один из них, то ложными будут предикат  , высказывания
, высказывания  ,
, 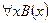 ,
, 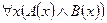 , то есть обе части принимают значение ложь.
, то есть обе части принимают значение ложь.
Из а) и б) следует равносильность 5.
Если в формуле А заменить связанную переменную другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, то получим формулу, равносильную А. Это правило называется переименование переменных связанных.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1078; Нарушение авторских прав?; Мы поможем в написании вашей работы!