Выполнимость формул логики предикатов

П. 4.4. Предваренная нормальная форма. Общезначимость и

Формула логики предикатов имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам. Используя равносильности алгебры высказываний и логики предикатов, каждую формулу логики предикатов можно привести к нормальной форме. Среди нормальных форм особое значение имеют предваренные нормальные формы.

Определение 4.16. Предваренной нормальной формой формулы логики предикатов называется такая нормальная форма, в которой либо полностью отсутствуют кванторные операции, либо они используются после всех операций алгебры логики.

Предваренную нормальную форму можно записать , где 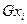понимается один из кванторов или 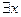, а формула А кванторов не содержит.

Если же все равны , то эта форма называется - формулой (или универсальной формулой); если же все равны , то эта форма называется - формулой. Если же существует такое, что суть , то такая форма называется скулемовской нормальной формой (или -формой).

Можно доказать, что всякая формула логики предикатов может быть приведена к равносильной ей предваренной форме.

Пример 15:

Привести к предваренной нормальной форме следующие формулы логики предикатов:

1. ;

2.

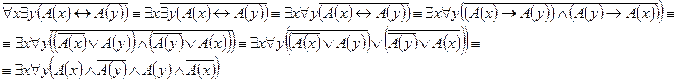
Определение 4.17. Формула логики предикатов называется выполнимой в области М (в данной интерпретации), если существует значение переменных, входящих в эту формулу из области М, при которых формула А принимает истинные значения.

Определение 4.18. Формула А называется выполнимой, если существует область, на которой эта формула выполнима.

Определение 4.19. Формула А называется тождественно истинной (тождественно ложной) в области М, если она принимает истинные значения (ложные значения) для всех для всех значений переменных из М, входящих в эту форму.

Определение 4.20. Формула А называется общезначимой, если она тождественно истинна во всякой области.

Общезначимую формулу называют логическим законом. Если формула А общезначима, то формула называется ложной или противоречием.

Задача распознавания общезначимости формул логики предикатов существенно сложнее, чем формул алгебры высказываний. Она называется проблемой разрешимости. В 1936 году американец математик А. Черг доказал, что в общем виде проблема разрешимости логики предикатов не имеет алгебраического решения.

Вопросы и задания.

1. Даны предикаты : "Человек х живет в Москве", 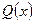: "Человек х преподает в школе". Прочтите словами следующие предикаты и укажите для каждого из них множество истинности:

а) ;

б) ;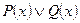

в) ;

г) ;

д) ;

е) ;

ж) .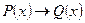

2. Даны предикаты 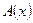: ""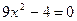 и 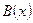: "". Найдите их множества истинности, если их область определения М есть:

а) ;

б) ;

в) .

3. Прочитайте следующие высказывания и определите, какие из них истинные, а какие ложные, считая, что все переменные пробегают множество действительных чисел:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

4. Изобразите на координатной прямой множества истинности следующих заданных на R одноместных предикатов:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .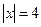

5. Выясните, равносильны ли следующие предикаты, если их рассматривать над множеством действительных чисел R, над множеством рациональных чисел Q, над множеством целых чисел Z и над множеством натуральных чисел N:

а) , ;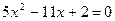

б) , ;

в) , ;

г) , ;

д) , ;

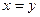е) , .

6. Определить, является ли один из следующих предикатов, заданных на множестве действительных чисел, следствием другого:

а) , ;

б) , ;

в) , ;

г) , ;

д) , .

7. Определить, какие из следующих выражений являются формулами логики предикатов, а какие нет, и объяснить почему:

а) ;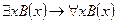

б) ;

в) ;

г) ;

д) ;

е) .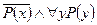

8. Предайте следующим формам указанные интерпретации и определите истинные значения получающихся высказываний:

а) 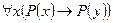, , : "Имя х состоит из 5 букв, ";

б) , интерпретация та же, что и для предыдущей формулы;

в) , , : "";

г) , , : "", .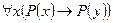

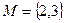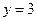9. Являются ли общезначимыми следующие формулы логики предикатов:

а) ;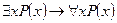

б) ;

в) ;

г) .

10. Привести к предваренной нормальной форме следующие формулы логики предикатов, считая P и Q бескванторными формулами:

а) ;

б) ;

в) ;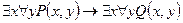

г) .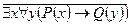

11. Привести к …. нормальной форме:

а) ;

б) .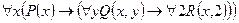

12. Доказать тождественную ложность формулы: .

Дата добавления: 2014-01-07