Первинні показники міжгалузевого балансу

Галузі виробництва (проміжне споживання)

Всього спожито

Невиробниче споживання

Нагромадження

Чистий вивіз (експорт)

Всього вироблено

...

n

Особисте

З фондів колективного споживання

Державне

Основні виробничі фонди

Оборотні кошти

Матеріальні витрати галузі:     . . . n

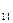x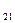 x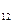

x   ...

...

...   ...

...   ...

...   ...

...   ...

...   ...

...

...   ...

...   ...

x   x

Всього матеріальних витрат

...

...

...

...

ПС

...

...

...

...

...

...

ССП

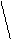Складові ВВП: 1.Оплата праці   2.Чистий прибуток   3. Споживання основного капіталу   4.Сальдо податків на виробництво. Валова додана вартість   5.Сальдо податків на продукти та імпорт ВВП........

...     ...

...     ...

...     ...

...     ...

ВДВ   ВВП

Продукція.....

x

x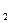

...

...

ССП

Границі квадрантів у таблиці позначені подвійними лініями, а номери – римськими цифрами.

У першому квадранті розглядаються міжгалузеві потоки, тобто обсяги продукції галузі – рядка, які споживаються галуззю-стовпчиком як частина її проміжного споживання (ПС). Наприклад, x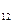- це кількість продукції галузі 1, яку спожито галуззю 2 з виробничою метою; x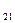- це кількість продукції галузі 2, яку споживає (для власного виробництва) галузь 1 тощо.

У підсумковому стовпчику “Всього спожито” подано обсяги виробничого споживання продукції кожної з галузей. Підсумковий рядок “Всього матеріальних витрат” містить дані про сукупні обсяги виробничого споживання продукції всіх видів кожною з галузей. Сума елементів підсумкового рядка має дорівнювати сумі елементів підсумкового стовпчика, це є величина проміжного споживання.

У другому квадранті подано галузеву та функціональну (за її призначенням) структуру кінцевого продукту. Визначено, скільки продукції кожної із галузей споживається із невиробничою метою населенням, державою та фондами колективного споживання (страхова медицина, страхова пенсійна система тощо), скільки продукції використано для створення нових основних виробничих фондів. До складу приросту оборотних коштів входить зміна запасів виробленої продукції. У цьому ж квадранті подано галузеву структуру чистого експорту.

У третьому квадранті наведено структуру доданої вартості кожної із галузей, підсумкові рядки ВДВ (валова додана вартість) та ВВП (валовий внутрішній продукт) визначають внесок кожної галузі у сукупну величину цих показників. У деяких балансах подано більш детальну структуру окремих складових доданої вартості, наприклад, окремими рядками визначено умовні та фактичні соціальні платежі. Підсумковий стовпчик “Всього вироблено” та рядок “Продукція” подають величини сукупного виробництва продукції кожної із галузей. У першому випадку вони обчислюються за обсягами використання виробленої продукції, у другому – за її вартістю.

У четвертому квадранті відсутні будь-які показники. У подальшому, можливо, він використовуватиметься для аналізу процесів перерозподілу створених прибутків та зв’язків між прибутками і кінцевим споживанням.

На основі початкових показників обчислюються наступні похідні показники:

а) коефіцієнти прямих витрат:

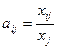, x_j - обсяг виробництва у j -й галузі (підсумковий стовпчик),

x_ij - міжгалузевий потік (з 1 квадранту, обсяг продукції і -ї галузі, використаний на споживання у галузі j)

б) кінцевий продукт галузі і:

(це береться з ІІ квадранту)

Показники x_j та y_i пов’язані наступними співвідношеннями.

1. З умов збалансованості виробництва та споживання у замкненій економіці випливає:

, ,

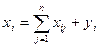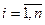за визначенням a_ij виконується: x_ij = a_ij x_j. Звідси

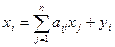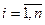, . (8.1)

2. У випадку відкритої економіки:

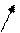
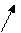
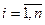, . (8.2)

Імпорт продукції і -ї галузі

Експорт продукції і -ї галузі

Рівняння (8.2) можна переписати у вигляді

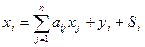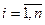, . (8.3)

	експортно-імпортне сальдо

Якщо вважати a_ij відомими, то системи (8.1)-(8.3) складаються з n рівнянь з 2 n, 4 n та 3 n параметрами відповідно. З них лише n можуть вважатися невідомими, інші мають бути визначені. У залежності від того, які змінні вважаються невідомими, є різні схеми розрахунків за цими рівняннями. Найбільш розповсюджені з них наступні:

1) для систем (8.1)-(8.3) треба визначити обсяги виробництва х = (х ₁,..., х_n) за відомими значеннями кінцевого продукту, експорту та імпорту (або експортно-імпортного сальдо).

Для цього треба розв’язати (відносно х) систему лінійних рівнянь виду

(Е - А)х = z,

де A = {a_ij}, Е - одинична матриця, z = (z ₁, …, z_n) – n -вимірний вектор з відомими значеннями компонент. Доведено, що така система має єдиний розв’язок х ≥ 0 за будь-яких z ≥ 0, якщо виконується умова

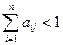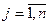, , або ж

, .

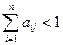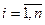Остання умова зветься умовою продуктивності матриці А. Перша її частина виконується, якщо додана вартість для кожної галузі – додатня. Дійсно, вартість продукції j -ї галузі, обчислена за стовпчиком таблиці первинних показників, буде дорівнювати:

,

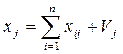за визначенням a_ij:

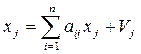, V_j > 0,

звідси

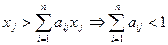
(якщо x_j > 0).

Крім рівнянь (8.1)–(8.3), для обсягів виробництва, невиробничого споживання, експорту та імпорту, мають місце відомі рівняння міжгалузевого балансу для цін

, ,

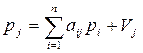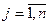де V_j – додана вартість, яка припадає на одиницю продукції галузі j, p_j – ціна на продукцію цієї ж галузі (якщо баланс - натуральний), або ж індекс галузевих цін по відношенню до тих, у яких було складено баланс (якщо він - вартісний).

У випадку, якщо ціна, за якою споживач і купує продукцію галузі j, відрізняється від ціни виробника у (1 + γ_ij) разів, рівняння цін набуватимуть вигляду

, .

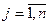За ними можна здійснювати обчислення, аналогічні до вищезгаданих.

Дата добавления: 2014-01-07