План лекции. 1. Понятие комплексного числа

ЛЕКЦИЯ 1

1. Понятие комплексного числа.

2. Комплексная плоскость. Тригонометрическая форма записи комплексных чисел.

3. Извлечение корня из комплексного числа.

4. Понятие области на комплексной плоскости.

ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

1. Комплексная плоскость. Тригонометрическая форма записи комплексного числа.

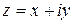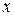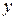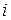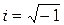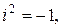
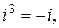
Комплексным числом называется выражение вида , где и действительные числа, - мнимая единица (), причем 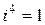и т.д.

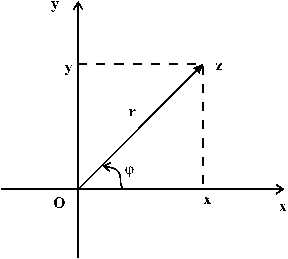Рассмотрим плоскость с прямоугольной декартовой системой координат. Такая плоскость называется комплексной. Точку на комплексной плоскости можно задать с помощью радиуса 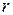и полярного угла .

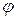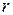- модуль комплексного числа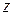 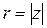, 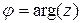; 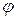- аргумент числа .

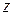За положительное направление угла 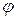принят отсчет против часовой стрелки от положительного направления оси .

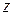Аргумент комплексного числа является неоднозначной величиной и задается с точностью до слагаемого кратного двум. В дальнейшем аргумент, как многозначную величину будем обозначать 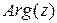, а для конкретности сохраним .

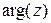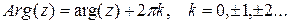
Главное значение аргумента: .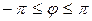

Из рисунка видно, что

;

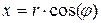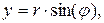
таким образом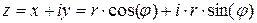

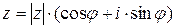- тригонометрическая форма записи комплексного числа.

;

; ; ;

;

;

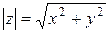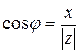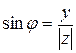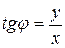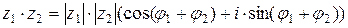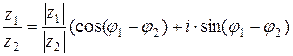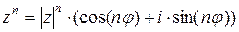- формула Муавра.

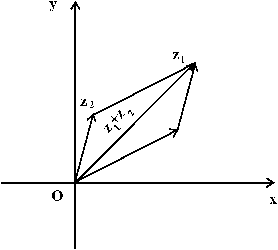
Точки на комплексной плоскости, а, следовательно, и комплексные числа можно задать с помощью вектора. При сложении и вычитании комплексных чисел используют общие правила сложения и вычитания векторов.

Извлечение корня из комплексного числа.

(*)

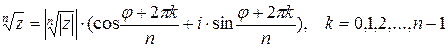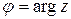
Пусть 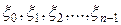- корни 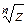. Из равенства (*) следует, что

(**)

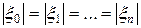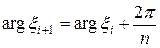
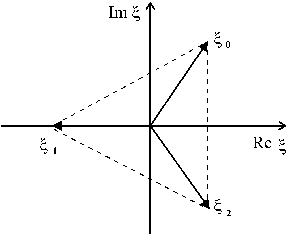
Из равенства (**) следует, что если комплексные корни изобразить на комплексной плоскости в виде вектора, то вершины этих векторов будут лежать в углах правильного 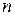-угольника, вписанного в окружность радиуса .

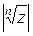Пример. Найдем корень третьей степени из числа –1.

; ;

;

;

, ;

,

, .

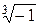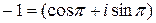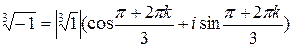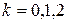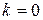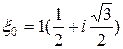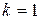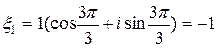
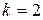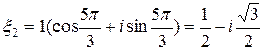ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

Дата добавления: 2014-01-07