Лекция 14

План лекции

1. Теорема о начальном и предельном значениях.

2. Применение преобразования Лапласа для решения дифференциальных уравнений.

3. Обратное преобразование Лапласа рациональной алгебраической дроби.

4. Изображение импульса произвольной формы. Изображение периодических функций.

10.Предельное значение оригинала.

Теорема 10.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), и если произведение s F(s) является аналитической функцией в правой полуплоскости на мнимой оси, то

.

Доказательство.

По теореме изображения производной

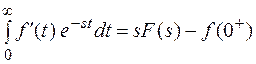
Перейдем пределу при 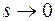, данный предел существует, т. к. функция sF(s) – аналитическая в окрестности 0. Получим

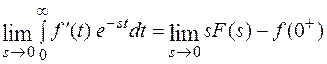
Переход к пределу под знаком интеграла возможен, т. к. по условию теоремы абсцисса абсолютной сходимости для функции , поэтому

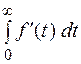- существует.

наименьшее α - абсцисса абсолютной сходимости.

Re s > , α < 0.

Из равенства

следует, что

.

Для функции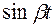

- не существует.

Теорема не справедлива, т. к. функция 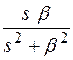имеет два полюса на мнимой оси.

Пример.

Найти 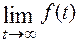, если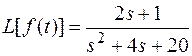

=

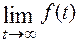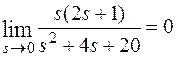
11.Начальное значение оригинала.

Теорема 11.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), то

при условии, что т. о., что Re s = c.

Доказательство.

По определению

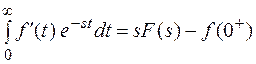
Перейдем к пределу

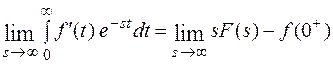
Покажем, что

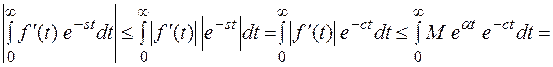
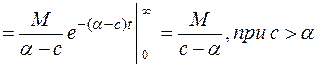
Справедливо равенство

Из равенства

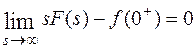
следует, что

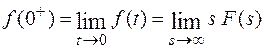
Дата добавления: 2014-01-07