Обратное преобразование Лапласа рациональной алгебраической дроби

ПРИМЕНЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.

Рассмотрим пример. Требуется решить уравнение

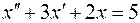
Обозначим .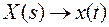

В соответствии с теоремой 2

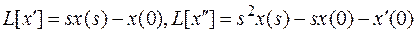
Пусть заданы начальные условия

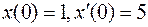
Применим к правой и левой частям уравнения преобразование Лапласа

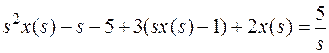
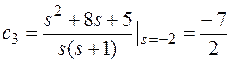
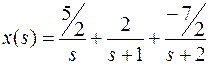
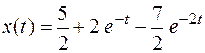
Изображение решения линейного дифференциального уравнения имеет вид

,

где - некоторые числа.

Если то дробь неправильная. Поделим числитель на знаменатель

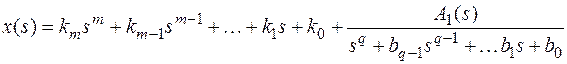
Принимая во внимание изображение и ее производной, получим

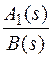- правильная дробь.

Т. о. задача заключается в нахождении обратного преобразования Лапласа от правильной дроби.

В соответствии с формулой обратного преобразования Лапласа

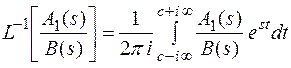
Для вычисления интеграла воспользуемся леммой Жордана. Рассмотрим замкнутый контур L, изображенный на рисунке.

L =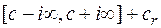

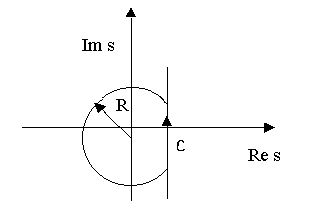
Вычеты берутся по всем точкам, лежащим левее прямой Re S = C.

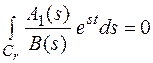
Тогда

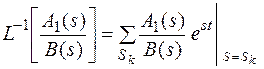
В соответствии с основной теоремой (1) изображение является аналитической функцией в области Re S > , т. к. C > , то все особые точки функции 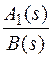лежат левее прямой Re S = C, т. е. вычеты необходимо брать по всем особым точкам.

Рассмотрим два частных случая.

1. B(s) = 0, имеет простые вещественные корни.

Обозначим корни уравнения B(s) = 0. Применяя формулу вычетов, найдем

2. Два корня являются мнимыми.

Пусть уравнение B(s) = 0, имеет корни

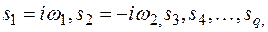
корни вещественные и простые.

Изображение такого вида имеет место, когда в правой части дифференциального уравнения стоит гармоническая функция: sin или cos.

Применяя формулу 3 вычетов, найдем

Два первых слагаемых комплексно сопряжены, поэтому при их суммировании мнимые части сокращаются, а вещественные удваиваются.

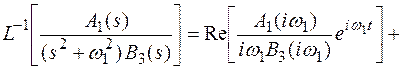
Иногда вместо операции взятия вещественной части удобно взять мнимую часть. Принимая во внимание, что

,запишем

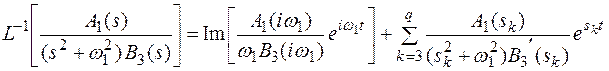
Замечание.

Полученные формулы можно использовать и в случае комплексных корней уравнения, однако в этом случае возникает необходимость выделять вещественную часть, что часто приводит к громоздким вычислениям. В этом случае целесообразно использовать разложение дроби на сумму простых дробей.

Дата добавления: 2014-01-07