Актуальное изучение системы

Актуальное изучение системы (как она есть сейчас) включает шаги №№ 1-4 (по табл.1).

Шаг №1: Какие у системы компоненты? Для этого составляется список №1 – полный перечень компонент системы 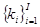. Далее формируется структура на базе списка №1, то есть определяется:

1.а. Как компоненты связаны между собой? Для этого составляется матрица: (список №1) x (список №1) – строки и столбцы которой поименованы именами элементов списка №1. Проставляя единицы в ячейках, определяющих связи между компонентами - получим структуру №1 – структуру системы 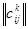здесь верхний индекс означает, что структура строится на компонентах системы. Для этого строится матрица вида:

	k1	k2		kI
k1	c11	c12		c1I
k2	c21	c22		c2I
kI	cI1	cI2		cII

Этому шагу соответствует матрица а) - 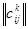на рис. 9. Строки и столбцы изображены как соответствующие оси на плоскости.

Шаг №2. Какие у системы надсистемы? Для этого составляется список №2 – полный перечень компонент надсистем 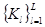. Далее формируются структуры на базе списка №1 и списка №2, то есть определяется:

2.а. Как надсистемы связаны друг с дружкой. Для этого составляется матрица: (список №2) х (список №2). Получим структуру №2 - 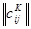в виде матрицы

	K1	K2		KL
K1	c11	c12		c1L
K2	c21	c22		c2L
KL	cL1	cL2		cLL

Этому шагу соответствует схема б) на рис. 9, где к матрице связей внутренних компонент 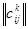добавлена плоскость с матрицей связей внешних компонент .

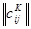2.б. Как надсистемы включают подсистемы данной системы? Для этого составляется матрица: (список №1) х (список №2). Получим структуру №3 – связь внутренних и внешних компонент системы 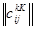- матрицу вида

	K1	K2		KL
k1	c11	c12		c1L
k2	c21	c22		c2L
kI	cI1	cI2		cIL:

Этому шагу анализа соответствует схема в) на рис. 9, где к плоскостям с матрицами смежности для внутренних 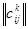и внешних компонент системы 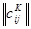добавлена матрица связи внутренних и внешних компонент системы .

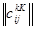Шаг №3. Какие у системы внутренние функции? Для этого составляется список №3 – полный перечень внутренних функций 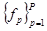. Далее формируется структуры на базе списка №3 - то есть определяется:

3.а. Как функции связаны между собой? Для этого составляется матрица 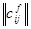: (список №3) х (список №3). Получим структуру №4 – структуру внутренних функций системы

	f1	f2		fP
f1	c11	c12		c1P
f2	c21	c22		c2P
fP	cP1	cP2		cPP

Результат этой процедуры представлен как матрица 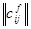в плоскости г) на рис. 9

3.б. Как внутренние функции 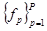- список №3 связаны с компонентами системы 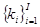- список №1?. Для этого составляется матрица (список №1) х (список №3). Получим структуру №5 - 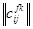- матрицу вида:

	f1	f2		fP
k1	c11	c12		c1P
k2	c21	c22		c2P
kI	cI1	cI2		cIP

Иллюстрацией этой процедуры является матрица 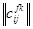в плоскости (f – k) на кубе матриц смежности системы ж) рис. 9

3.в. Как внутренние функции 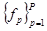- список №3 связаны с надсистемами системы 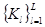- список №2. Для этого составляется матрица: (список №2) х (список №3). Получим структуру №6 - 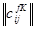- матрицу вида:

	f1	f2		fP
K1	c11	c12		c1P
K2	c21	c22		c2P
KL	cL1	cL2		cLP

Иллюстрацией этой процедуры является матрица 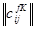в плоскости (f – K) на кубе матриц смежности системы ж) рис. 9.

Шаг №4. Какие у системы внешние функции? Для этого составляется список №4 – полный перечень внешних функций 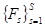. Далее формируются структуры на базе списка №3 и списка №4, то есть определяется:

4.б. Как надфункции 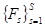связаны друг с дружкой? Для этого составляется матрица 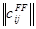: (список №4) x (список №4). Получим структуру №7:

	F1	F2		FS
F1	c11	c12		c1S
F2	c21	c22		c2S
FS	cS1	cS2		cSS

Иллюстративно этому соответствует схема д) на рис. 9 и выглядит как добавление к плоскости (f – f), в которой лежит матрица смежности внутренних функций системы 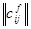, плоскости (F – F), в которой лежит матрица смежности внешних функций системы .

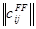4.а. Как надфункции 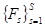подключены к функциям 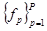данной системы? Для этого составляется матрица 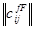: (список №3) х (список №4). Получим структуру №8 – связь внутренних и внешних функций системы:

	f1	f2		fP
F1	c11	c12		c1P
F2	c21	c22		c2P
FS	cS1	cS2		cSP

Иллюстративно этому соответствует схема е) на рис. 9 и выглядит как добавление к плоскости (f – f), в которой лежит матрица смежности внутренних функций системы 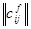, и плоскости (F – F), в которой лежит матрица смежности внешних функций системы 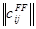, третьей, в которой лежит матрица смежности внешних и внутренних функций системы .

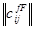4.в. Как надфункции 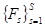- список №4 связаны с компонентами системы 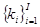- список №1?. Для этого составляется матрица (список №1) х (список №4). Получим структуру №9 - 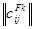- матрицу вида:

	F1	F2		FS
k1	c11	c12		c1S
k2	c21	c22		c2S
kI	cI1	cI2		cIS

Этой процедуре соответствует матрица смежности 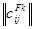в плоскости (F – k) на схеме ж) рис. 9.

4.г. Как надфункции 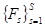- список №4 связаны с надсистемами 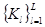- список №2?. Для этого составляется матрица (список №2) х (список №4). Получим структуру №10 - 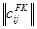- матрицу вида:

	F1	F2		FS
K1	c11	c12		c1S
K2	c21	c22		c2S
KL	cL1	cL2		cLS

Этой процедуре соответствует матрица смежности 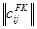в плоскости (F – K) на схеме ж) рис. 9.

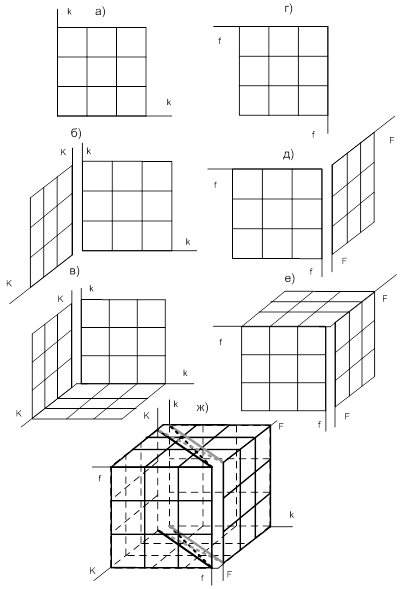
Рис. 9.

Итак, проведен структурно-функциональный анализ существующей системы. Получены матрицы, на основе которых могут быть построены собственно структура системы – множество ее компонент со связями, функциональные структуры, компонентно-функциональные структуры – всего 10 структур. Но при анализе мы использовали определение функция, как внешнего проявления свойств объекта в данной системе отношений, определённый способ взаимодействия объекта с окружающей средой. Для того, чтобы представить систему, как процессное единство необходимо представить структуры №№ 5,6,9,10 в форме процессных схем. При этом каждая из компонент системы может быть или входной или выходной для некоторого преобразования. Но компоненты в свою очередь могут содержать в себе сеть процессов, обеспечивающих выполнение функции компоненты в системе. Для раскрытия этих особенностей привлекаются компоненты (объекты) и преобразования (действия), не замеченные при первоначальном анализе. Как список компонент и их детализация (декомпозиция), так и список преобразований и их декомпозиция принципиально открыты, то есть могут пополняться, уточняться, детализироваться.

Дата добавления: 2014-01-07