Основные уравнения электростатики

ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ

Пример применения MATLAB

Задача.

Дано: Имеется треугольная поверхность в пространстве. Координаты вершин заданы. Значения векторов напряжённости электрического и магнитного поля в вершинах также заданы. Сторонняя составляющая напряжённости электрического поля равна нулю.

Требуется вычислить электромагнитную мощность, проходящую через эту треугольную поверхность. Составить функцию MATLAB, выполняющую это вычисление. При вычислениях считать, что вектор положительной нормали направлен так, что если смотреть из его конца, то движение в порядке возрастания номеров вершин будет происходить против часовой стрелки.

Решение. Ниже приведён текст m-функции.

% em_power_tri - вычисление электромагнитной мощности, проходящей через

% треугольную поверхность в пространстве

% P=em_power_tri(nodes,E,H)

% ВХОДНЫЕ ПАРАМЕТРЫ

% nodes - квадратная матрица вида [x1, x2, x3; y1, y2, y3; z1, z2, z3].',

% в каждой строке которой записаны координаты соответствующей вершины.

% E - матрица компонентов вектора напряжённости электрического поля в вершинах:

% строкам соответствуют вершины, столбцам - декартовы компоненты.

% H - матрица компонентов вектора напряжённости магнитного поля в вершинах.

% ВЫХОДНОЙ ПАРАМЕТР

% P - электромагнитная мощность, проходящая через треугольник

%

% При вычислениях предполагается, что на треугольнике

% векторы напряжённости поля изменяются в пространстве по линейному закону.

function P=em_power_tri(nodes,E,H);

% Вычисляем вектор двойной площади треугольника

S=[det([ones(3,1) nodes(:,[2,3])]) det([ones(3,1) nodes(:,[3,1])]) det([ones(3,1) nodes(:,[1,2])])];

P=sum(cross(E,(ones(3,3)+eye(3))*H,2))*S.'/24;

Пример запуска разработанной m-функции:

>> nodes=2*rand(3,3)

nodes =

0.90151 0.5462 0.4647

1.4318 0.50954 1.6097

1.7857 1.7312 1.8168

>> E=2*rand(3,3)

E =

0.46379 0.15677 1.6877

0.47863 1.2816 0.3478

0.099509 0.38177 0.34159

>> H=2*rand(3,3)

H =

1.9886 0.62843 1.1831

0.87958 0.73016 0.23949

0.6801 0.78648 0.076258

>> P=em_power_tri(nodes,E,H)

P =

0.18221

Если предположить, что пространственные координаты измеряются в метрах, вектор напряжённости электрического поля – в вольтах на метр, вектор напряжённости магнитного поля – в амперах на метр, то в данном примере электромагнитная мощность, проходящая через треугольник, получилась равной 0.18221 Вт.

Электростатическим называют постоянное поле неподвижных электрических зарядов. Источниками электростатического поля являются свободные электрические заряды и электрические диполи. В электростатическом поле отсутствует сторонняя составляющая напряженности электрического поля E _c.

В соответствии со сказанным уравнения электростатики в интегральной форме имеют вид

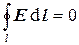
Уравнения электростатики в дифференциальной форме

(1)

В случае линейных изотропных диэлектрических свойств среды уравнение материальной связи между векторами E и D имеет вид:

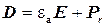(2)

Дата добавления: 2014-01-07