Граничные условия для векторов электростатического поля

На поверхности раздела сред, где или P _r изменяются скачком, справедливы следующие соотношения

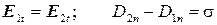
На поверхности проводящего тела

Тангенциальная составляющая вектора напряженности электрического поля непрерывна на любой поверхности раздела сред.

Скачок нормальной составляющей вектора электрического смещения равен поверхностной плотности электрических зарядов.

Скалярный электрический потенциал. Краевая задача анализа электростатического поля

Поле вектора E является безвихревым, поэтому его можно представить в виде градиента некоторого скалярного поля

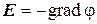, (3)

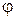– скалярный электрический потенциал.

Подставив соотношение (3) в (2), а затем (2) в (1), получим

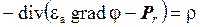
или

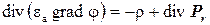(4)

Уравнение (4) является уравнением электростатики относительно скалярного электрического потенциала. Это уравнение является основой для постановки краевой задачи анализа электростатического поля.

Для обеспечения единственности решения уравнения (4) необходимо дополнить его граничными условиями для искомого потенциала или для нормальной составляющей вектора электрического смещения на поверхности, ограничивающей расчетную область, т.е.

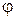= поверхностное распределение – на части граничной поверхности Г₁,

D _n = поверхностное распределение – на части граничной поверхности Г₂,

Г = Г₁ + Г₂ – замкнутая граничная поверхность.

Первое граничное условие называется граничным условием первого рода (иногда его называют граничным условием Дирихле). Второе граничное условие называется граничным условием второго рода (иногда его называют граничным условием Неймана).

Если задавать только граничные условия Неймана, то единственность решения будет обеспечена только с точностью до постоянной (однородной) составляющей скалярного поля .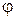

В случае однородного распределения диэлектрической проницаемости среды и вектора остаточной поляризованности среды уравнение (4) может быть записано в виде

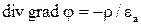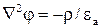или (5)

Дата добавления: 2014-01-07