
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример эргодического случайного процесса
|
|
|
|
Условия эргодичности
Необходимым и достаточным условием эргодичности стационарного случайного процесса является так называемая метрическая транзитивность процесса.
Стационарный случайный процесс метрически транзитивен, если любая часть совокупности реализаций процесса, вероятностная мера которой меньше единицы, не сохраняет свойство стационарности. Напротив, если указанная часть реализации процесса сохраняет свойство стационарности, то процесс не является метрически транзитивным и не является эргодическим.
Рассмотрим снова гармоническое колебание (2.7), у которого амплитуда и частота постоянные, а фаза – случайная величина, распределенная равномерно на интервале 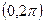 . Как было показано в п.2.10, это колебание представляет стационарный в узком смысле случайный процесс.
. Как было показано в п.2.10, это колебание представляет стационарный в узком смысле случайный процесс.
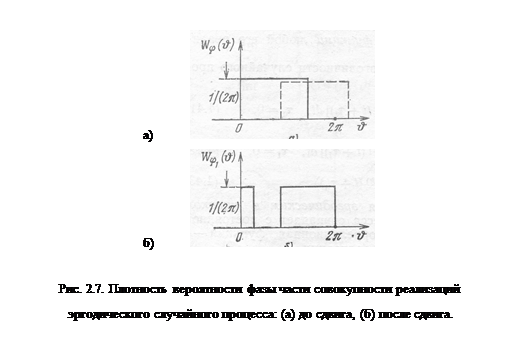
Выделим часть совокупности реализаций процесса (2.7), определяемую неравенством  (рис. 2.7,а).
(рис. 2.7,а).
 |
Вероятность попадания значений случайной фазы в указанный диапазон
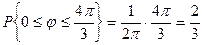
меньше единицы.
Выясним, сохраняет ли свойство стационарности рассматриваемая часть совокупности реализаций. Заменяя переменную  и полагая
и полагая 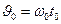 , получаем для указанной части совокупности реализаций смещенную плотность вероятности, изображенную на рис. 2.7,а штриховой линией. Вследствие неразличимости двух значений фаз, отличающихся на
, получаем для указанной части совокупности реализаций смещенную плотность вероятности, изображенную на рис. 2.7,а штриховой линией. Вследствие неразличимости двух значений фаз, отличающихся на 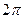 , указанная смещенная плотность вероятности приобретает вид, изображенный на рис. 2.7,б, который существенно отличается от исходной плотности вероятности (рис. 2.7,а, сплошная линия). Это означает, что для рассматриваемой части совокупности реализаций процесса (2.7) свойство стационарности не сохранилось и, следовательно, исходный стационарный случайный процесс является эргодическим.
, указанная смещенная плотность вероятности приобретает вид, изображенный на рис. 2.7,б, который существенно отличается от исходной плотности вероятности (рис. 2.7,а, сплошная линия). Это означает, что для рассматриваемой части совокупности реализаций процесса (2.7) свойство стационарности не сохранилось и, следовательно, исходный стационарный случайный процесс является эргодическим.
Однако не каждый стационарный случайный процесс является эргодическим. В качестве примера рассмотрим гармоническое колебание (2.7) с постоянной частотой 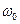 , но случайной фазой
, но случайной фазой 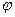 , равномерно распределенной на интервале
, равномерно распределенной на интервале 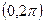 , и независимой от фазы случайной амплитудой
, и независимой от фазы случайной амплитудой 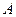 , распределенной по рэлеевскому закону. Причем, значение амплитуды
, распределенной по рэлеевскому закону. Причем, значение амплитуды 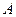 колебания изменяется от одной реализации к другой, но остаётся неизменным на интервале наблюдения одной реализации. Как отмечалось в п.2.10, такое колебание сохраняет свойство строгой стационарности.
колебания изменяется от одной реализации к другой, но остаётся неизменным на интервале наблюдения одной реализации. Как отмечалось в п.2.10, такое колебание сохраняет свойство строгой стационарности.
Вероятностная мера такого случайного процесса определяется полной вероятностью вида:
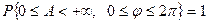 .
.
Выделим часть совокупности реализаций этого стационарного случайного процесса, которая определяется неравенствами 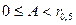 и
и  , где
, где  – медиана рэлеевского распределения. Для выделенной таким образом части совокупности реализаций
– медиана рэлеевского распределения. Для выделенной таким образом части совокупности реализаций
 .
.
Однако так как инвариантность функций распределения рассматриваемого процесса относительно сдвига времени  определяется инвариантностью к сдвигу только распределения фазы, то стационарность сохраняется и для указанной части совокупности реализаций (с вероятностной мерой, равной 0,5). Следовательно, гармоническое колебание со случайной амплитудой и равномерно распределенной фазой является стационарным, но не эргодическим случайным процессом. Нетрудно убедиться, что для этого колебания среднее по времени квадрата случайного процесса зависит от выбора реализации и принимает различные значения для различных реализаций. Например, если усредняются по времени следующие две реализации:
определяется инвариантностью к сдвигу только распределения фазы, то стационарность сохраняется и для указанной части совокупности реализаций (с вероятностной мерой, равной 0,5). Следовательно, гармоническое колебание со случайной амплитудой и равномерно распределенной фазой является стационарным, но не эргодическим случайным процессом. Нетрудно убедиться, что для этого колебания среднее по времени квадрата случайного процесса зависит от выбора реализации и принимает различные значения для различных реализаций. Например, если усредняются по времени следующие две реализации: 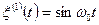 и
и 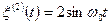 , то
, то  и
и 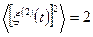 .
.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 3903; Нарушение авторских прав?; Мы поможем в написании вашей работы!