Эргодические случайные процессы

Стационарный в узком смысле случайный процесс называется эргодическим, если любая его вероятностная характеристика, полученная усреднением по множеству реализаций, с вероятностью, сколь угодно близкой к единице, равна временному среднему, полученному усреднением за достаточно большой промежуток времени из единственной реализации случайного процесса. Поэтому для определения вероятностных характеристик эргодического случайного процесса нет необходимости изучать совокупность реализации, а достаточно одной реализации, наблюдаемой в течение длительного промежутка времени.

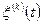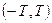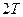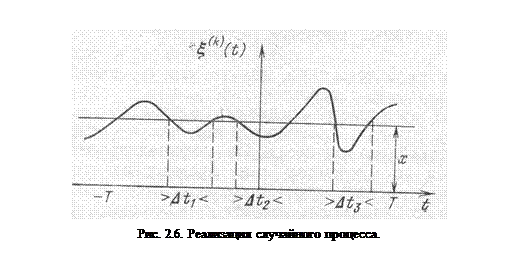
Рассмотрим некоторую реализацию случайного процесса на интервале времени . За период суммарное время пребывания реализации ниже порога 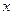(рис. 2.6) будет определяться выражением

,

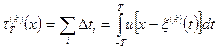где 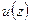– функция единичного скачка.

Предел

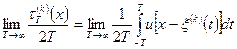
называется относительным временем пребывания реализации 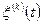ниже порога .

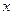Для эргодического процесса относительное время пребывания ниже порога любой реализации равно одномерной функции распределения стационарного случайного процесса

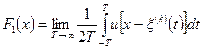. (2.8)

Дифференцируя обе части выражения (2.8) по 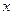, находим

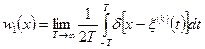, (2.9)

где 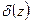– дельтофункция.

Из (2.9) можно записать выражение для момента 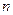-го порядка эргодического процесса:

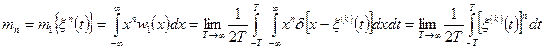. (2.10)

Обозначая символом 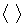усреднение по времени, получаем соотношение

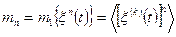, (2.11)

которое устанавливает равенство между моментом 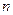-го порядка эргодического процесса и усреднением по времени 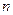-й степени произвольно выбранной реализации этого процесса.

В частности, величину 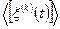можно трактовать как постоянную составляющую реализации, которая равна среднему значению эргодического процесса:

.

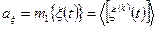Если 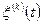представляет собой изменение напряжения или тока на нагрузке 1 Ом, то квадрат 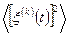равен средней мощности (квадрату эффективного значения) реализации. Поэтому в соответствии с (2.11) можно записать

,

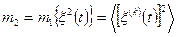т. е. средний квадрат эргодического случайного процесса равен средней мощности любой его реализации.

Соотношения (2.8) и (2.9) обобщаются на двумерную функцию распределения и двумерную плотность вероятности

,

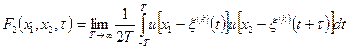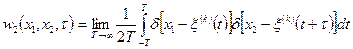. (2.12)

Из (2.10) и (2.11) следует выражение для корреляционной функции

,

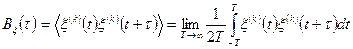т. е. корреляционная функция эргодического случайного процесса равна временной корреляционной функции любой его реализации.

Стационарный процесс называется эргодическим в широком смысле, если среднее значение процесса совпадает с постоянной составляющей его реализации, а корреляционная функция – с временной корреляционной функцией реализации.

Дата добавления: 2014-01-06