Стационарные случайные процессы

Лекция 3.

Случайный процесс называется стационарным (в узком смысле), если для любого значения функция распределения 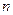-го порядка процесса удовлетворяет тождеству

. (2.4)

Иными словами, случайный процесс стационарен в узком смысле тогда и только тогда, когда функции распределения любого порядка не зависят от начала отсчета времени, т. е. когда любые вероятностные характеристики инвариантны относительно сдвига переменной .

Можно сформулировать ряд необходимых (но не достаточных) условий стационарности в узком смысле. Если хотя бы одно из них не выполняется, то можно утверждать, что исследуемый процесс – нестационарный.

Итак, полагая в (2.4) , получаем одно из необходимых условий стационарности

, (2.5)

т. е. для стационарности процесса необходимо, чтобы его одномерная функция распределения не зависела от времени. Из (2.5) следует, что необходимыми условиями стационарности является также независимость от времени одномерной плотности вероятности процесса, а, следовательно, и моментных функций . В частности, самыми простыми необходимыми условиями стационарности являются постоянство среднего значения и дисперсии процесса.

Полагая в (2.3) и , получаем еще одно необходимое условие стационарности

. (2.6)

т. е. для стационарности процесса необходимо, чтобы его двумерная функция распределения зависела не от двух моментов времени, а только от их разности. Из (2.6) следует, что необходимыми условиями стационарности являются также зависимости только от разности двух моментов времени двумерных плотности вероятности , а, следовательно, и корреляционной функции

, .

Дата добавления: 2014-01-06