Пример стационарного в узком смысле случайного процесса

Рассмотрим случайный процесс , представляющий гармоническое колебание, у которого амплитуда и частота постоянные, а фаза — случайная величина:

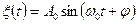. (2.7)

Покажем, что необходимым и достаточным условием стационарности в узком смысле является равномерное распределение фазы

, .

Любая конечномерная функция распределения процесса (2.7) полностью определяется распределением случайной фазы. Поэтому для доказательства инвариантности функции распределения процесса относительно сдвига переменной необходимо и достаточно доказать указанную инвариантность для распределения случайной фазы.

Пусть . Тогда из (2.7) следует

, , .

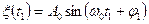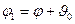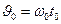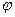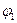Плотность вероятности случайной фазы процесса и случайной фазы процесса 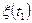после временного сдвига изображены сплошными линиями на рис. 2.4,а,б. Так как фазы, отличающиеся на 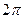, не изменяют значений процесса, то 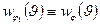, т. е. равномерная плотность вероятности фазы инвариантна сдвигу процесса во времени (штриховая линия на рис. 2.4,б). Но при неравномерном распределении фазы случайный процесс (2.7) перестает быть стационарным, как это иллюстрируют рис. 2.5,а,б (плотность вероятности, изображенная штриховой линией на

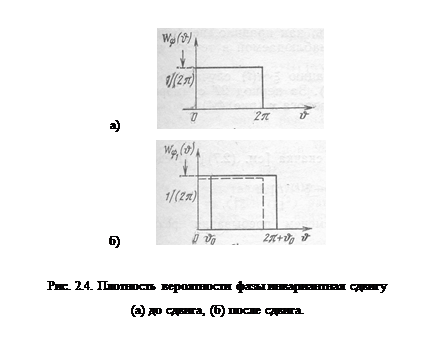рис. 2.5,б не совпадает с исходной плотностью вероятности, изображенной на рис. 2.5,а).

Заметим, что при равномерном распределении случайной фазы процесс (2.7) сохраняет свойство стационарности в узком смысле и тогда, когда амплитуда 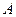становится случайной величиной, не зависящей от времени, так как в этом случае инвариантность функций распределения процесса относительно сдвига определяется только инвариантностью к сдвигу распределения фазы.

Дата добавления: 2014-01-06