Формирующий фильтр

Из выражения (4.17) следует, что стационарный в широком смысле случайный процесс с заданной корреляционной функцией 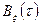может быть получен как реакция на воздействие белого шума единичной интенсивности 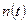линейной системы с импульсной характеристикой 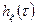. При этом импульсная характеристика 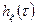такой системы будет однозначно связана с корреляционной функцией 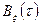искомого процесса и будет удовлетворять следующему интегральному уравнению.

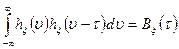. (4.19)

Линейную систему с такой импульсной характеристикой 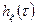называют формирующим фильтром.

Таким образом, для определения импульсной характеристики 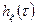формирующего фильтра необходимо решить интегральное уравнение (4.19).

Вместо решения интегрального уравнения (4.19) импульсную характеристику формирующего фильтра можно найти через передаточную функцию 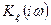этого фильтра. Передаточная функция 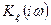формирующего фильтра однозначно связана со спектральной плотностью мощности искомого процесса, и может быть найдена из следующего уравнения

.

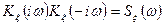Таким образом, задача определения передаточной функции 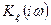формирующего фильтра сводится к факторизации функции 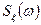, т. е. к разложению ее на два сомножителя .

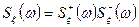Процесс на выходе произвольной линейной системы с известной импульсной характеристикой 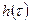, когда на ее выходе действует процесс , можно сформировать исходя из интегрального выражения

.

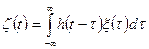Поэтому процесс можно рассматривать как реакцию на входной белый шум 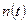линейной системы, представляющей последовательное соединение формирующего фильтра и данной произвольной линейной системы (рис. 4.4):

,

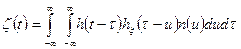или как реакцию на воздействие белого шума 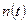линейной системы с импульсной характеристикой (рис. 4.5):

.

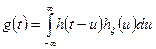Дата добавления: 2014-01-06