Узкополосные линейные системы

Линейные радиотехнические системы, работающие на высоких и промежуточных частотах как правило являются узкополосными [2]. Поэтому особенный интерес вызывает вопрос прохождения белого шума через узкополосную линейную систему. Перед тем как рассмотреть этот вопрос, необходимо определить, что понимается под узкополосной линейной системой.

Итак, если частотная характеристика линейной системы имеет резко выраженную область резонанса в окрестности частоты 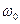и если , где – ширина полосы пропускания частотной характеристики системы, то линейная система с такой характеристикой называется узкополосной.

Заменой переменной интегрирования 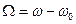приводим формулу (4.5) для импульсной характеристики линейной системы, к следующему виду

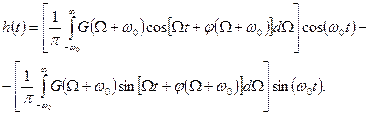(4.20)

Для узкополосной системы нижние пределы интегрирования в интегралах, заключенных в фигурные скобки, с малой погрешностью можно распространить до 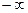[1]. Тогда, обозначая

,

,

,

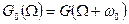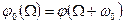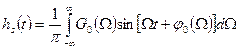
можно переписать выражение (4.20) в следующем виде

, (4.21)

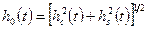где и .

Если частотная характеристика симметрична, а фазовая – антисимметрична относительно резонансной частоты 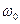, то 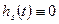, и импульсная характеристика узкополосной линейной системы примет вид:

.

В этом случае импульсная характеристика узкополосной системы представляет собой медленно меняющуюся функцию 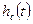с высокочастотным гармоническим заполнением (рис. 4.5).

Ширина полосы пропускания узкополосной линейной системы

.

Дата добавления: 2014-01-06