Определение огибающей и фазы квазигармонического колебания

Лекция 8.

При воздействии стационарного белого шума на линейную радиотехническую систему, работающую на высоких и промежуточных частотах, на выходе такой системы образуется случайны процесс, по виду напоминающий модулированное гармоническое колебание . Это квазигармоническое колебание можно представить в виде узкополосного случайного колебания, т. е. в виде гармонического сигнала, случайно модулированного по амплитуде и фазе:

,

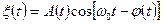где 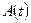и 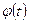– медленно меняющиеся функции по сравнению с .

Чем уже полоса пропускания линейной системы, тем она инерционнее и тем медленнее будут меняться случайные огибающая и фаза. При этом средняя частота высокочастотного заполнения будет равна резонансной частоте 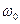. Поэтому в некоторых задачах со случайным процессом можно оперировать, так же как модулированным гармоническим колебанием. Для этого колебание необходимо представить в другом виде

,

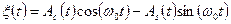где 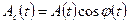и .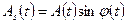

Отсюда следует, что

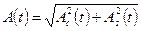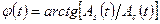, . (4.25)

Формулы (4.25) позволяют интерпретировать 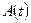как длину, а 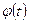угол поворота вектора, проекции которого на оси прямоугольной системы координат равны 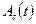и 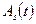. Возможные значения фазового угла 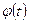между осью абсцисс и направлением вектора ограничены интервалом .

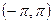Длина вектора 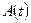и его фазовый угол 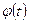изменяются во времени случайным образом, так что конец вектора совершает случайные блуждания на плоскости. При такой интерпретации проекци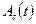и и 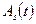естественно назвать квадратурными компонентами процесса .

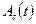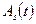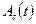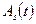В литературе [3] указывается, что если исходный процесс является гауссовским (нормальным), то квадратурные компоненты и являются совместно нормальными. Если в дополнение к этому процесс стационарен и имеет нулевое математическое ожидание, то процессы и являются стационарными и стационарно связанными. А их математические ожидания равны нулю.

Необходимо отметить, что значения квадратурных компонент, взятые в один и тот же момент времени, всегда не коррелированны и, следовательно, для гауссовского стационарного процесса , независимы. При этом дисперсии компонент одинаковы и равны дисперсии процесса

.

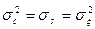Для получения статистических характеристик узкополосного случайного процесса необходимо построить законы распределения огибающей 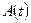и фазы 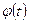процесса . Если принять, что исходный случайный процесс на входе узкополосной системы является стационарным гауссовским белым шумом с нулевым математическим ожиданием, то можно сравнительно просто найти совместную плотность распределения вероятности огибающей 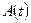и фазы .

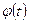Задача нахождения плотности вероятности огибающей и фазы узкополосного гауссовского случайного процесса полностью совпадает с задачей нахождения плотности вероятности длины и угла поворота вектора, квадратурные компоненты которого независимы и распределены нормально.

Дата добавления: 2014-01-06