Плотность вероятности модуля и фазы случайного вектора на плоскости

Рассмотрим преобразование двух случайных величин следующего вида:

, . (4.26)

Это преобразование взаимно однозначное, причем 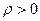, а возможные значения случайной величины 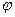заключены в пределах . Геометрически преобразование (4.26) означает переход от случайных декартовых координат точки к её случайным полярным координатам: модулю 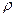и фазе 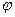случайного вектора. Этот вектор выходит из начала координат, а конец вектора совпадает с точкой .

Обратное преобразование координат имеет следующий вид:

, .

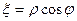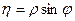Геометрическое представление перехода из декартовой в полярную систему координат:

;

.

Для перехода зададим элементарные приращения с условием, что площади .

В окрестности точки мы получим две элементарные площадки. Отсюда вероятности попадания вектора в обеих системах равны.

,

следовательно

,

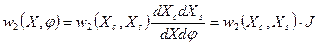где 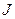– якобиан преобразования от декартовых координат к полярным.

Определим, чему равен якобиан? Из равенства площадей следует:

.

.

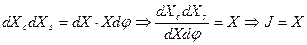Совместная плотность вероятности огибающей и фазы узкополосного шума:

.

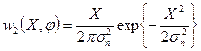Математический подход при переходе из декартовой в полярную систему координат.

Пусть задана двумерная функция распределения случайных декартовых координат 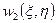, и надо найти совместную функцию распределения полярных координат .

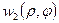Любая точка в Эвклидовом пространстве принадлежит некоторой области, площадь которой можно выразить как в декартовой , так и в полярной системе координат . Предел отношения этих площадей при переходе от одних координат к другим, когда 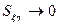и , равен якобиану преобразования

.

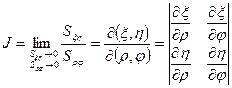Тогда совместная плотность вероятности 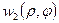находится из выражения

.

Так как якобиан преобразования

,

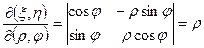то при взаимно однозначном преобразовании случайных величин получим

, , .

Есл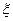и и независимы, то

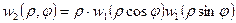, , . (4.27)

Плотность вероятности модуля и фазы может быть найдена из выражений

, . (4.28)

, . (4.29)

Дата добавления: 2014-01-06