КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы первого метода Ляпунова
|
|
|
|
Они позволяют судить об устойчивости состояния равновесия нелинейной системы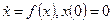 
(20.14)
по уравнению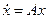
(20.15)
полученному линеаризацией функции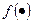 
в точке 
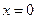(замечание: 
).
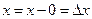Теорема 20.4. Если все собственные значения матрицы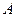 
находятся в левой полуплоскости, то состояние 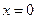системы (20.14) асимптотически устойчиво. Таким образом, отброшенные при линеаризации члены не могут сделать систему неустойчивой.
Теорема 20.5. Если среди собственных значений матрицы 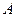хотя бы одно находится в правой полуплоскости, то состояние 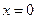системы (20.14) неустойчиво.
Теорема 20.6. Если среди собственных значений матрицы 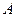хотя бы одно имеет нулевую вещественную часть, то по уравнению (20.15) нельзя судить об устойчивости состояния 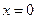системы (20.14). Таким образом, надо анализировать уравнение (29.14).
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 285; Нарушение авторских прав?; Мы поможем в написании вашей работы!