Стационарность

Отклик зависимой переменной на единичное приращение независимой переменной (устойчивость моделей, содержащих авторегрессионые члены)

Рассмотрим отклик зависимой (эндогенной) переменной 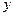на единичное приращение независимой (экзогенной) переменной .

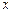Рассмотрим две модели:

1. ;
2. .

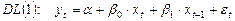Рассмотрим отклик за один краткосрочный период (short-run), то есть мы не рассматриваем лаговые члены. Для первой модели имеем:

при ,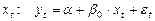

при ,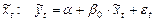

где — единичное приращение независимой переменной.

Тогда отклик зависимой переменной 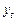имеет вид:

.

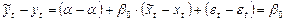Для второй модели отклик :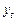

при ,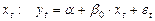

при ,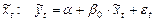

.

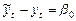То есть отклик зависимой переменной один и тот же.

Рассмотрим отклик зависимой переменной в долгосрочном периоде (long-run), то есть рассматриваем также и все лаговые переменные. Другими словами находим отклик зависимой переменной, которая является суммарным влиянием всех экзогенных переменных.

Для первой модели отклик равен:

,

,

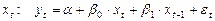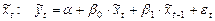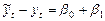
Для второй модели:

,

.

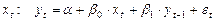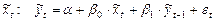В данном случае получить отклик по вышеуказанной схеме не удается. Поэтому преобразуем второе уравнение, чтобы избавиться от 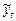в правой части

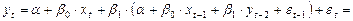
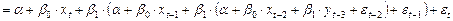
Отдельно выпишем члены, которые будут участвовать в отклике: константы сократятся и учитывать будем только члены, содержащие независимые переменные .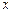

,

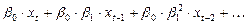тогда сам отклик будет формироваться следующим образом:

,

.

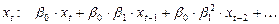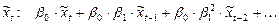В пределе отклик будет иметь вид:

.

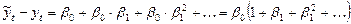Правая часть выражения — бесконечная геометрическая прогрессия. Сумма геометрической прогрессии может быть посчитана только тогда, когда прогрессия убывающая, то есть 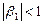. В таком случае, применив формулу суммы геометрической прогрессии, получим:

,

.

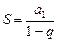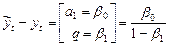Таким образом, для того чтобы отклик был конечным, необходимо, чтобы 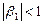. Это и есть условие устойчивости временного ряда.

То есть при исследовании отклика временного ряда необходимо в первую очередь обращать внимание на коэффициент перед первой лагированной объясняющей переменной. Если условие устойчивости выполняется (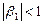), отклик будет конечным. В противном случае — бесконечным.

Понятие стационарности — более точное по сравнению с понятием устойчивости (но более трудно проверяемое). Стационарность различают двух видов:

• Строгая Стационарность (стационарность в узком смысле — strictly stationary SS);
• Слабая Стационарность (стационарность в широком смысле — weak stationary WS).

Определение SS: Ряд 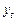строго стационарен, если совместное распределение 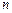наблюдений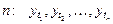

не зависит от сдвига по времени , то есть совпадает с распределением

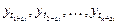для любых .

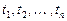На практике чаще используется понятие слабой стационарности или стационарности в широком смысле.

Определение WS: Ряд 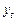слабо стационарен, если его среднее, дисперсия и ковариация не зависят от момента времени .

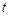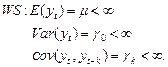
Ковариация зависит от лага, а не от момента времени.

Пример стационарного процесса — белый шум (white noise), помехи:

, ~ .

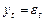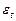Рис.2 Белый Шум (White Noise)

Упражнение 1:

Показать, что white noise — стационарный ряд.

Упражнение 2:

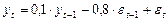
Является ли этот ряд стационарным? Ответ обоснуйте.

Примером нестационарного процесса является случайное блуждание (random walk).

Дата добавления: 2014-01-06