Пример. Передаточная функция фильтра рис

Передаточная функция фильтра рис. 1.2.4: H(z) = b₀/(1-a₁z). При а₁= 0.5 полюс знаменателя: z_р= 2. |z_р|>1. Фильтр устойчив.

Передаточная функция фильтра рис. 1.2.5: H(z) = b₀/(1+a₁z). При а₁= 1.1 полюс знаменателя: z_р= -0.909. |z_р| < 1. Фильтр неустойчив, что и подтверждает пример фильтрации.

Передаточная функция фильтра рис. 1.2.6: H(z) = 0.5(1+z)/(1-z). Полюс знаменателя: z_р= 1. В принципе, фильтр неустойчив, но эта неустойчивость проявляется только при k = ∞. Импульсный отклик фильтра h(n) = {0.5,1,1,1, ….}, сумма которого равна ∞ только при n = ∞, т.е. при интегрировании бесконечно больших массивов. При интегрировании конечных массивов результат всегда конечен.

Приведенный критерий устойчивости относится к несократимой дроби, т.к. в противном случае возможна компенсация полюса нулем передаточной функции и следует проверить наличие однозначных нулей и полюсов.

Проверка на устойчивость требуется только для рекурсивных цифровых фильтров (систем с обратной связью), нерекурсивные системы всегда устойчивы.

1.5. Частотные характеристики фильтров /л2,л13,л24/.

Общие понятия. От z-образов сигналов и передаточных функций подстановкой z = exp(-jwDt) в уравнение (1.4.2) можно перейти к Фурье-образам функций, т.е. к частотным спектрам сигналов и частотной характеристике фильтров, а точнее – к функциям их спектральных плотностей.

Можно применить и способ получения частотных характеристик непосредственно из разностного уравнения системы обработки данных. Так как цифровая фильтрация относится к числу линейных операций, то, принимая для сигнала на входе фильтра выражение x(kDt) = B(w) exp(jwkDt), мы вправе ожидать на выходе фильтра сигнал y(kDt) = A(w) exp(jwkDt). Подставляя эти выражения в разностное уравнение фильтра (1.2.1), получаем:

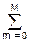a_m A(w) exp(jwkDt-jwmDt) =b_n B(w) exp(jwkDt-jwnDt).

A(w) exp(jwkDt)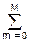a_m exp(-jwmDt) = B(w) exp(jwkDt)b_n exp(-jwnDt).

A(w)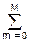a_m exp(-jwmDt) = B(w)b_n exp(-jwnDt). (1.5.1)

Передаточная частотная функция (частотная характеристика при а_о=1):

H(w) = A(w)/B(w) =b_n exp(-jwnDt)[1+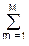a_m exp(-jwmDt)]. (1.5.2)

Нетрудно убедиться, что полученная частотная характеристика повторяет функцию (1.4.2) при z = exp(-jwDt), что и следовало ожидать. Аналогично z-преобразованию (1.4.7), частотная характеристика фильтра представляет собой Фурье-образ его импульсной реакции, и наоборот. При Dt = 1:

H(w) =h(n) exp(-jwn), (1.5.3)

h(n) = (1/2p)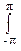H(w) exp(jwn) dw. (1.5.4)

В общем случае H(w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой (АЧХ), а аргумент j(w) - фазочастотной характеристикой (ФЧХ).

A(w) = |H(w)| =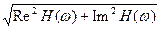

j(w) = arctg(-Im H(w)/Re H(w)).

На рис. 1.5.1-1.5.3 приведены частотные характеристики фильтров (модули и аргументы спектральных плотностей), которые были рассмотрены выше в примерах и на рис. 1.2.4 – 1.2.6. Графики приведены в границах главных диапазонов спектров и получены непосредственной подстановкой z=exp(-jwDt) при Dt=1 в уравнения передаточных функций H(z).

Рис. 1.5.1. Спектр не имеет особых точек.

Рис. 1.5.2. Спектр имеет особые точки на границах диапазонов.

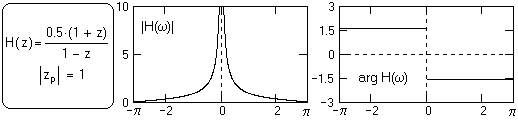
Рис. 1.5.3. Спектр интегрирующего фильтра. Особая точка на нулевой частоте.

При обработке ограниченных массивов амплитуда центрального пика равна количеству точек массива.

Основные свойства частотных характеристик фильтров:

1. Частотные характеристики являются непрерывными функциями частоты.

2. При дискретизации данных по интервалам Dt функция H(w) является периодической. Период функции H(w) равен частоте дискретизации входных данных F = 1/Dt. Первый низкочастотный период (по аргументу w от -p/Dt до p/Dt, по f от -1/2Dt до 1/2Dt) называется главным частотным диапазоном. Граничные частоты главного частотного диапазона соответствуют частоте Найквиста ±w_N, w_N = p/Dt. Частота Найквиста определяет предельную частоту обработки данных.

3. Для фильтров с вещественными коэффициентами импульсной реакции h(nDt) функция АЧХ является четной, а функция ФЧХ - нечетной. С учетом этого частотные характеристики фильтров обычно задаются только на интервале положительных частот 0-w_N главного частотного диапазона. Значения функций на интервале отрицательных частот являются комплексно сопряженными со значениями на интервале положительных частот.

Как правило, при частотном анализе фильтров значение Dt интервала дискретизации принимают за 1, что соответственно определяет задание частотных характеристик на интервале (0,p) по частоте w или (0,1/2) по f. При использовании быстрых преобразований Фурье (БПФ) вычисления спектров осуществляются в одностороннем варианте положительных частот в частотном интервале от 0 до 2p (от 0 до 1 Гц), где комплексно сопряженная часть спектра главного диапазона (от -p до 0) занимает интервал от p до 2p (для ускорения вычислений используется принцип периодичности дискретных спектров). Заметим, что при выполнении БПФ количество точек спектра равно количеству точек входной функции, а следовательно отсчет на частоте 2p, комплексно сопряженный с отсчетом на частоте 0, отсутствует. При нумерации точек входной функции от 0 до N он принадлежит точке N+1 - начальной точке следующего периода, при этом шаг по частоте равен 2p/(N+1). Современное программное обеспечение БПФ допускает любое количество точек входной функции, при этом для нечетного значения N частоте p соответствует отсчет на точке (N+1)/2, не имеющий сопряженного отсчета, а при четном значении N отсутствует отчет на частоте p (она располагается между отсчетами k=N/2 и N/2 +1). Отсчетам с номерами k главного диапазона БПФ (за исключением точки k=0) соответствуют комплексно сопряженные отсчеты N+1-k (за исключением точки k=(N+1)/2 при нечетном N).

Фазовая и групповая задержка. Задержка сигналов во времени относится к характерной особенности каузальных систем в целом, а, следовательно, рекурсивных и односторонних нерекурсивных фильтров.

Фазовая задержка, это прямая характеристика временной задержки фильтром гармонических колебаний. При подаче на вход фильтра гармоники sin wt, сигнал на выходе каузального фильтра, без учета изменения его амплитуды, равен sin(wt-j), при этом:

sin(wt-j) = sin w(t-t_p), ωt-j = ω(t-t_p).

Отсюда, фазовая задержка t_p на частоте w равна:

t_p = j /ω. (1.5.5')

При распространении (1.5.5) в целом на спектральную передаточную функцию фильтра получаем:

t_p(w)= j(w) /ω. (1.5.5)

Постоянство значения t_p(w) в определенном частотном диапазоне обеспечивает для всех гармоник сигнала такое же соотношение их фазовых характеристик, какое было на входе системы, т.е. не изменяет формы сигнала, если его спектр полностью сосредоточен в этом частотном диапазоне и значения АЧХ в этом диапазоне также имеют постоянное значение. Это условие является определяющим, например, для систем передачи данных, для сглаживающих и полосовых частотных фильтров.

Что касается каузальных фильтров, то они, как правило, имеют в рабочем диапазоне определенную зависимость значения t_p от частоты, которая характеризуется групповым временем задержки (ГВЗ).

Допустим, что сигнал на входе фильтра представляет собой сумму двух гармоник с близкими частотами:

s(t) = cos ω₁t + cos ω₂t.

Тождественная тригонометрическая запись:

s(t) = 2 cos[0.5(ω₁+ω₂)t] · cos[0.5(ω₁-ω₂)t].

Эта запись показывает, что сумму двух гармоник с частотами ω₁ и ω₂ можно рассматривать, как амплитудную модуляцию гармоники с частотой (ω₁+ω₂)/2 гармоникой с частотой (ω₁-ω₂)/2. При прохождении через фильтр каждая из гармоник ω₁ и ω₂ может получить различную задержку, при этом сигнал на выходе фильтра, без учета амплитудных изменений:

s(t) = cos (ω₁t-j₁) + cos(ω₂t-j₂).

Тождественная запись:

s(t) = 2 cos[0.5((ω₁+ω₂)t-(j₁+j₂))] · cos[0.5((ω₁-ω₂)t-(j₁-j₂))].

Пульсацию колебаний выразим через групповую временную задержку t_g:

cos[0.5((ω₁-ω₂)t-(j₁-j₂))] = cos[0.5(ω₁-ω₂)·(t-t_g)].

Отсюда:

(ω₁-ω₂)·t_g = j₁-j₂.

t_g = (j₁-j₂)/(ω₁-ω₂) = Dj /Dω. (1.5.6)

При распространении этого выражения на непрерывную частотную характеристику фильтра:

t_g(ω)= dj(w)/dω. (1.5.7)

Для вычислений ГВЗ удобно использовать комплексный логарифм передаточной функции фильтра:

Ln(H(ω)) = ln |H(ω)| + j·j(ω), j(ω) = Im[Ln(H(ω)].

t_g(ω)= dj /dω = Im{d[Ln(H(ω))]/dω} = Im{dH(ω)/[H(ω)dω]}. (1.5.8)

Приближение для дискретных спектральных функций:

t_g(k·Dω) ≈ (2/Dω)·Im{(H_k+1-H_k) / (H_k+1+H_k }. (1.5.9)

1.6. Фильтрация случайных сигналов /л4,л15,л24/.

Если сигнал на входе фильтра является детерминированным, то его соотношение с выходным сигналом однозначно определяется импульсным откликом фильтра. Таким же однозначным является соотношение входа - выхода и для случайных сигналов, однако в силу природы последних аналитическое представление как входного сигнала, так и отклика системы, не представляется возможным. Для описания реакции фильтра на случайный входной сигнал используется статистический подход. Если параметры входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход фильтра поступает реализация случайного стационарного сигнала x(k·Dt) с нулевым средним, которая вызывает сигнал y(k·Dt) на выходе фильтра. Значение Dt, как обычно, принимаем равным 1.

Допустим, что фильтр имеет импульсный отклик h(n) = exp(-a·n), n ³ 0. Зададим на входе фильтра стационарный квазидетерминированный случайный сигнал, который не обладает свойством эргодичности, но имеет все свойства случайного сигнала и может быть описан в явной математической форме:

x(k) = A + cos(2·k+j),

где A и j - взаимно независимые случайные величины, причем значение j равномерно распределено в интервале [0, 2p]. При этом выходной сигнал определится выражением:

y(k) = h(n) _* x(k-n) º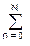h(n)×x(k-n) = A/3 + [3·cos(2k+j) + 2·sin(2k+j)]/13.

Из этого выражения следует, что выходной сигнал фильтра также является случайным и содержит те же самые случайные параметры, что и входной сигнал, а, следовательно, для него существуют определенные статистические характеристики.

Математическое ожидание произвольного входного случайного стационарного сигнала x(k) на выходе фильтра определится выражением:

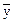= М{y(k)}= M{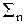h(n)·x(k-n)}=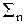M{x(k-n)}×h(n) =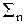h(n) =·К_пс. (1.6.1)

Отсюда следует, что математическое ожидание выходных сигналов фильтра равно математическому ожиданию входных сигналов, умноженному на коэффициент усиления фильтром постоянной составляющей. При К_пс = 1 среднее значение выходных сигналов не изменяется и равно среднему значению входных сигналов. Если фильтр не пропускает постоянную составляющую сигналов (сумма коэффициентов импульсного отклика фильтра равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание.

Корреляционные соотношения. Для центрированных входных сигналов x(k) размером (0-К) функция автокорреляции (ФАК) вычисляется по формуле:

R_x(n) = [1/(K+1-n)]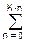x(k)·x(k+n).

По аналогичной формуле может быть вычислена и ФАК выходных сигналов. Для произведения выходных сигналов y(k) и y(k+n), образующих функцию автокорреляции выходных сигналов, можно также записать:

y(k)×y(k+n) = 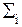h(i)h(j) x(k-i)x(k+n-j).

Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в правой части под знаками сумм

M{x(k-i) x(k+n-j)} = -R_x(k-i-k-n+j) = R_x(n+i-j),

получим:

R_y(n) =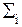h(i)h(j) R_x(n+i-j) º R_x(n) _* h(n+i) _* h(n-j). (1.6.2)

Таким образом, функция автокорреляции выходного сигнала равна ФАК входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом фильтра, что сохраняет четность ФАК выходного сигнала. Для нецентрированных процессов аналогичное заключение действительно и для ковариационных функций. На рис. 1.6.1 приведен пример ФАК входной и выходной случайных последовательностей при фильтрации RC-фильтром, форма импульсного отклика которого также приведена на рисунке.

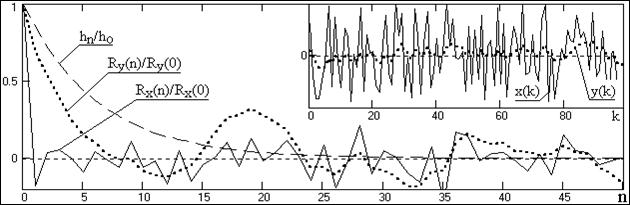
Рис. 1.6.1. Функции корреляционных коэффициентов.

Заметим, что для свертки импульсных откликов, производя замену n-j = m, мы имеем равенство:

h(n+i) _* h(n-j) = h(m+i+j) _* h(m) = h(m) _* h(m+p) = K_h(m),

где K_h(m) - функция ковариации импульсного отклика фильтра. Отсюда:

R_y(n) = R_x(n) _* K_h(m). (1.6.2')

Это означает появление в случайном сигнале на выходе фильтра определенной корреляционной зависимости, определяемой инерционностью фильтра. Эффективный интервал t_k корреляции данных в сигнале тем меньше, чем выше верхняя граничная частота w_в его спектра (по уровню 0.5):

t_к = p/w_в =1/2f_в.

Оценка интервала корреляции для конечных (непериодических) функций, как правило, производится непосредственно по функциям автокорреляции R(n):

t_k = 2·S_n|R(n)/R(0)| - 1,

где значение n ограничивается величиной 3-5 интервалов спада центрального пика до величины порядка 0.1×R(0) (дальше обычно начинаются статистические флюктуации значения R(n) около нулевой линии, вызванные ограниченностью выборки). Без такого ограничения за счет суммирования модуля флюктуаций, не несущих информациии, значение t_k завышается относительно расчетного по спектральной характеристике сигнала.

Рис. 1.6.2. Функции корреляционных коэффициентов большой выборки.

Функция R_x(n) случайных статистически независимых отсчетов близка к d-функции, свертка которой с K_h(m) приведет к формированию на выходе выходного сигнала, форма ФАК которого будет стремиться к форме K_h(m). При достаточно большой выборке случайных отсчетов входного сигнала это означает практически полное повторение функцией R_y(n) формы ковариационной функции импульсного отклика, как это можно видеть на рис. 1.6.2, который отличается от рис. 1.6.1 только количеством выборки К=10000. Соответственно, интервал корреляции выходных сигналов для случайной входной последовательности можно определять непосредственно по функции ковариации импульсного отклика фильтра:

t_k = 2·S_n|Kh(n)/Kh(0)| - 1, n ≥ 0.

Для взаимной корреляционной функции (ВКФ) R_xy входного и выходного сигналов соответственно имеем:

x(k)_*y(k+n) =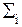h(i) x(k)·y(k+n-i).

R_xy(n) =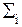h(i) R_x(n-i) º h(i) _* R_x(n-i). (1.6.3)

т.е. функция взаимной корреляции входного и выходного сигналов равна свертке ФАК входного сигнала с функцией импульсного отклика фильтра. Заключение действительно и для функций ковариации.

Другая взаимно корреляционная функция R_yx может быть получена из соотношения:

R_yx(n) = R_xy(-n) º h(i) _* R_x(n+i). (1.6.3')

Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике (h(i) = 0 при i<0) функция R_xy(n) также является односторонней и равна 0 при n<0, а функция R_yx соответственно равна 0 при n>0.

Спектр мощности выходного сигнала. Если на вход фильтра с импульсным откликом h(k) ó H(f) поступает случайный стационарный эргодический сигнал x(k) ó X_Т(f), имеющий на интервале Т функцию автокорреляции R_x(n) и спектр мощности W_x(f), то на выходе фильтра регистрируется стационарный эргодический сигнал y(k) ó Y_T(f) = X_Т(f)H(f). Соответственно, энергетический спектр выходного сигнала на том же интервале:

|Y_T(f)|² = |X_T(f)|² |H(f)|². (1.6.4)

Оценка спектра мощности (спектральной плотности энергии):

W_y(f)» (1/T) |X_Т(f)|² |H(f)|²= W_x(f) |H(f)|². (1.6.5)

Спектр мощности сигнала на выходе фильтра равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности корреляционных функций спектр мощности выходного сигнала также является четной действительной функцией и не имеет фазовой характеристики процесса.

Спектр мощности сигнала и его функция автокорреляции связаны преобразованием Фурье:

R_y(n) ó |Y(w)|² = W_y(w).

Дисперсия выходного сигнала (средняя мощность) определяется с использованием формулы (1.6.5):

s_y² = R_y(0) =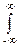W_x(f) |H(f)|² df º R_x(0)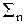h²(n) = s_x²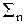h²(n). (1.6.6)

Если сигнал нецентрированный и значение дисперсии входного сигнала неизвестно, то по аналогичным формулам вычисляется сначала средний квадрат выходного сигнала или так называемая средняя мощность сигнала:

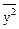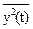== R_y(0) º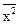 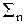h²(n) º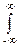W_x(f) |H(f)|² df, (1.6.7)

Вывод: средняя мощность выходного сигнала равна средней мощности входного сигнала, умноженной на сумму квадратов коэффициентов импульсного отклика фильтра. Для центрированных случайных сигналов средняя мощность равна дисперсии сигналов. Для нецентрированных выходных сигналов:

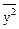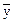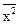s_y² = - ² º (-²)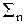h²(n). (1.6.8)

Взаимный спектр мощности входного и выходного сигнала:

W_xy(f)» (1/T)X_T(f)Y_T(f) = (1/T)|X_T(f)|² H(f) = W_x(f)H(f). (1.6.9)

Осуществляя преобразование Фурье левой и правой части выражения, получаем:

R_xy(n) = R_x(n) _* h(n), (1.6.10)

что повторяет формулу (1.6.3).

Усиление шумов. Критерием качества при использовании любого метода фильтрации информации можно считать выполнение целевого назначения с минимальным усилением шумов (максимальным их подавлением). Обозначим через e(k) аддитивный шум во входном сигнале с математическим ожиданием M{e(k)}= 0 и дисперсией s². Значения e(k) статистически независимы. С учетом помехи во входном сигнале значение сигнала на выходе:

y(k) = S_n h(n)[x(k-n)+e(k-n)].

Математическое ожидание значений выходного сигнала:

M{y(k)}= S_n h(n)[x(k-n)+M{e(k-n)]}= S_n h(n)x(k-n).

Вычислим дисперсию распределения отсчетов выходного сигнала:

D{y(k)}= M{[S_n h(n)[x(k-n)+e(k-n)]-M{y(k)}]²}=

= M{[S_n h(n) e(k-n)]²}= S_n h²(n) M{e²(k-n)}= s² S_n h²(n). (1.6.11)

Отсюда следует, что сумма квадратов значений импульсного отклика цифрового фильтра представляет собой коэффициент усиления шумов, равномерно распределенных в главном частотном диапазоне фильтра, в процессе фильтрации сигнала. Это полностью соответствует прямому использованию выражения (1.6.7) при W_x(f) = s²:

s_y² = s²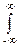|H(f)|² df ≡ s²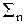h²(n). (1.6.11')

Таким образом, коэффициент усиления фильтром дисперсии статистически распределенных шумов при расчете по импульсному отклику:

K_q = 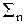h²(n). (1.6.12)

По дискретной передаточной функции фильтра:

K_q = [1/(N+1)] S_n H_n². (1.6.12')

Пример. Сглаживающий фильтр: y(k) = 0.2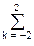x(k-n).

Коэффициент усиления шумов: 5 (0,2²) = 0,2. Дисперсия шумов уменьшается в 1/0.2 = 5 раз.

Выполните расчет коэффициента усиления шумов для пятиточечного фильтра МНК.

Контрольный ответ: 0.486.

Функция когерентности входного и выходного сигналов фильтра оценивается по формуле:

g_xy²(f) = |W_xy(f)|²/[W_x(f)×W_y(f)]. (1.6.12)

Если функции W_x(f) и W_y(f) отличны от нуля и не содержат дельта-функций, то для всех частот f значения функции когерентности заключены в интервале:

0 £ g_xy²(f) £ 1.

Для исключения дельта-функции на нулевой частоте (постоянная составляющая сигнала) определение функции когерентности производится по центрированным сигналам. Для фильтров с постоянными параметрами функция когерентности равна 1, в чем нетрудно убедиться, если в формулу (1.6.12) подставить выражения W_xy и W_y, определенные через W_x. Для совершенно не связанных сигналов функция когерентности равна нулю. Промежуточные между 0 и 1 значения могут соответствовать трем ситуациям:

1. В сигналах (или в одном из них) присутствует внешний шум (например, шум квантования при ограничении по разрядности).

2. Фильтр не является строго линейным. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений, при накоплении ошибки в рекурсивных системах и т.п.

3. Выходной сигнал y(t) помимо x(t) зависит еще от каких-то входных или внутренних системных процессов.

Величина 1-g_xy²(f) задает долю среднего квадрата сигнала y(t) на частоте f, не связанную с сигналом x(t).

Использование функций когерентности в практических методах анализа случайных данных подробно рассмотрено в работе /л4/.

1.7. Структурные схемы цифровых фильтров /л8,л21/.

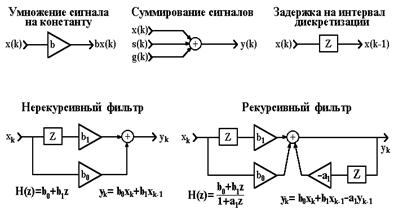Рис. 1.7.1. Структурные схемы цифровых фильтров.

Структурные схемы. Алгоритмы цифровой фильтрации сигналов (цифровых фильтров) представляются в виде структурных схем, базовые элементы которых показаны на рисунке 1.7.1 вместе с примерами структурных схем фильтров. Как правило, структурные схемы соответствуют программной реализации фильтров на ЭВМ, но не определяют аппаратной реализации в специальных радиотехнических устройствах, которая может существенно отличаться от программной реализации.

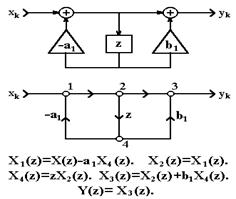Рис. 1.7.2. Граф фильтра.

Графы фильтров. Наряду со структурной схемой фильтр может быть представлен в виде графа, который отображает диаграмму прохождения сигналов и состоит из направленных ветвей и узлов.

Пример структурной схемы фильтра с передаточной функцией H(z) = (1+b₁z)/(1+a₁z) и графа, ей соответствующего, приведен на рисунке 1.7.2. С каждым i - узлом графа связано значение сигнала x_i(k) или его образа X_i(z), которые определяются суммой всех сигналов или z-образов входящих в узел ветвей. В каждой ij - ветви (из узла i в узел j) происходит преобразование сигнала в соответствии с передаточной функцией ветви, например задержка сигнала или умножение на коэффициент.

Соединения фильтров. Различают следующие соединения фильтров.

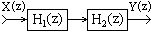Рис. 1.7.3.

1. Последовательное соединение (рис. 1.7.3). Выходной сигнал предшествующего фильтра является входным для последующего. Эквивалентная передаточная функция общей системы равна произведению передаточных функций фильтров, в нее входящих: H(z) = H₁(z)×H₂(z)×...×H_N(z).

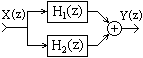Рис. 1.7.4.

2. Параллельное соединение (рис. 1.7.4). Сигнал подается на входы всех параллельно соединенных фильтров одновременно, выходные сигналы фильтров суммируются. Эквивалентная передаточная функция общей системы равна сумме передаточных функций фильтров, в нее входящих: H(z) = H₁(z)+H₂(z)+...+H_N(z).

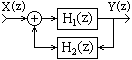Рис. 1.7.5.

3. Соединение обратной связи (рис. 1.7.5). Выходной сигнал первого фильтра подается на выход системы и одновременно на вход фильтра обратной связи, выходной сигнал которого суммируется, со знаком плюс или минус в зависимости от вида связи (отрицательной или положительной), с входным сигналом системы. Эквивалентная передаточная функция системы: H(z) = H₁(z)/(1±H₁(z)H₂(z)).

Схемы реализации фильтров. По принципам структурной реализации фильтров различают следующие схемы:

Рис. 1.7.6.

1. Прямая форма (рис. 1.7.6) реализуется непосредственно по разностному уравнению

y_k =b_nx_k-n –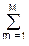a_my_k-m,

или по передаточной функции

H(z) =b_nzⁿ /(1+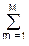a_mz^m).

2. Прямая каноническая форма содержит минимальное число элементов задержки. Передаточную функцию РЦФ можно представить в следующем виде:

H(z) = Y(z)/X(z) = H₁(z)H₂(z),

H₁(z) = V(z)/X(z) = 1/(1+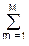a_mz^m),

H₂(z) = Y(z)/V(z) =b_nzⁿ.

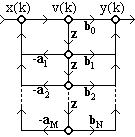Рис. 1.7.7.

Отсюда: v(k) = x(k) -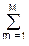a_mv(k-m), (1.7.1)

y(k) =b_nv(k-n). (1.7.2)

В разностных уравнениях (1.7.1-1.7.2) осуществляется только задержка сигналов v(k). Граф реализации РЦФ в прямой канонической форме приведен на рисунке 1.7.7.

3. Каскадная (последовательная) форма соответствует представлению передаточной функции в виде произведения:

H(z) =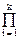H_i(z).

H_i(z) - составляющие функции вида (1-r_iz)/(1-p_iz) при представлении H(z) в факторизованной форме, где r_i и p_i - нули и полюсы функции H(z). В качестве функций H_i(z) обычно используются передаточные функции биквадратных блоков - фильтров второго порядка:

H_i(z) = (b_0i + b_1i ×z + b_2i ×z²) / (1 + a_1i ×z + a_2i ×z²).

4. Параллельная форма используется много реже и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.

Рис. 1.7.8.

Обращенные формы. В теории линейных направленных сигнальных графов существуют процедуры преобразования исходных графов с сохранением передаточных функций. Одна из таких процедур - обращение (транспозиция) графов, которая выполняется путем изменения направления всех ветвей цепи, при этом вход и выход графа также меняются местами. Для ряда систем такая транспозиция позволяет реализовать более эффективные алгоритмы обработки данных. Пример обращения графа прямой канонической формы рекурсивной системы (с перестроением графа на привычное расположение входа с левой стороны) приведен на рис. 1.7.8.

Дата добавления: 2014-01-07