
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция №1
|
|
|
|
Максвеллдың теңдеулері.
Физика курсынан бізге толық ток теңдеуі белгілі:

 (1)
(1)
Токты біз тығыздық арқылы жаза аламыз
 (2)
(2)
Осыдан
 (3)
(3)
Үшінші теңдеуді бірінші теңдеуге кіргіземіз
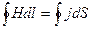 (4)
(4)
Төртінші теңдеудің сол жағын Стокс теоремасы арқылы көлем интегралына ауыстырамыз
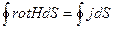 (5)
(5)
Аудан бойынша екі интеграл тең, сол себептен
 (6)
(6)
Бұл теңдеуді Максвелл былай түсінген:
Мангнит өрісі тоқ тығыздығын тудырады сым бойында, ал конденсатордың екі бет арасында заряд ағыны байқалған емес, сонда қандай ток тығыздығы туралы сөз болу
керек? Ал Максвелл болса конденсатордың екі бетінің арасында ығысу тоғы жүреді деп санайды. Ығысу токтың тығыздығын Максвелл былай анықтаған:

 =
=  (7)
(7)
Немесе:
 (8)
(8)
Бұл теңдеуді Максвеллдың бірінші заңы немесе бірінші теңлеуі деп санаймыз.
Ал енді электр өрісін қарастырайық. Заряды +q материалдық нүктенің электр өрісінің кернеулігі
 (9)
(9)
Eнді осы зарядты сфера ішіне тығып қояйық, сонда электр өрісінің күш сызықтары сфера бетін тесіп өтеді. Электр кернеулігінің толық ағынын табайық – ол сфераны тесіп өтетін электр күш сызықтарының санын береді.
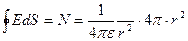 (10)
(10)
Сонымен электр кернеулігінің толық ағыны
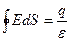 (11)
(11)
Енді зарядты тығыздық арқылы табайық
 (12)
(12)
Немесе
 (13)
(13)
Енді (13) теңдеудің сол жағын Остроградский- Гаусс теоремасы арқылы өңдейік
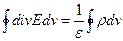 (14)
(14)
Егер интегралдар бір біріне тең болса, онда интеграл астындағы шамалар да тең болмақ
 (15)
(15)
Енді элект кернеулігінен ығысу векторына ауысайық
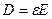 ,
, 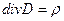 (16)
(16)
Соңғы (16) формула Максвеллдың үшінші теңдеуі боп саналады.
Енді Фарадей заңына көшейік  (17)
(17)
Ф - магнит ағыны.  (18)
(18)
Ал енді Э.Қ.К пен курнеулік арасындағы байланысты табайық
 (19)
(19)
Немесе
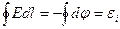 (20)
(20)
(17) және (20) формулалар арасында қандай байланыс бар?
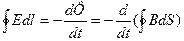 (21)
(21)
Соңғы теңдеудің сол жағын Стокс теоремасымен өңдейік
 (22)
(22)
Cоңғы формуланың оң жағында дифференциал мен интегралдың орнын ауыстырайық
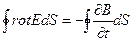 (23)
(23)
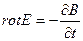 (24)
(24)
Cоңғы формула Фарадейдің екінші теңдеуі боп саналады
Төртінші теңдеу жеке магнит зарядтарының жоқтығын білдіреді cебебі магнит күш сызықтары тұйық.
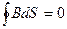 (25)
(25)
 , (26)
, (26)
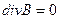 (27)
(27)
Соңғы екі теңдеулер Максвеллдың төртінші заны боп саналады
Дәріс №2
Максвелл теңдеулері комплекс түрінде
Максвелл теңдеулерін комплекс түрінде жазу үшін алдымен электр және магнит кернеуліктерін комплекс түрінде анықтап алайық.
Егер электр және мегнит өрістері синус не косинус заңдарымен өзгеретін болса онда:
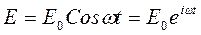 (1)
(1)
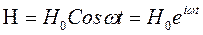 (2)
(2)
Кернеуліктер комплекс түрінде болған соң E, H төбесіне нүкте қоятын боламыз Ė, Ĥ. Маквеллдың бірінші теңдеуі былай жазылады:
 (3)
(3)
Мұнда
 (4)
(4)
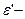 комплексті диэлектрикалық өтімділік.
комплексті диэлектрикалық өтімділік.
 (5)
(5)
Дәл солай rotE табамыз
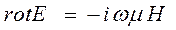 (6)
(6)
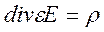 (7)
(7)
Максвеллдың төртінші теңдеуі
 (8)
(8)
Монохроматик өрісінің үзіліссіз теңдеудің түрі осындай:
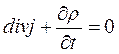 (9)
(9)
Комплекс түрінде былай болады:
 (10)
(10)
Біртекті және изотропты орта үшін  координаттардан тәуелді емес. Сол себептен
координаттардан тәуелді емес. Сол себептен
 (11)
(11)
 (12)
(12)
Сонымен изотропты орта үшін келесі теңдеулер жүесі жеткілікті
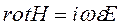 (13)
(13)
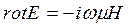 (14)
(14)
анизотропты орта үшін 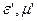 - тензор болады
- тензор болады
 (15)
(15)

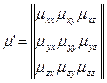 (16)
(16)
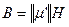 (17)
(17)
 (18)
(18)
 (19)
(19)
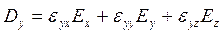 (20)
(20)
 (21)
(21)
Меншікті өткізгіш  те тензор
те тензор
 (22)
(22)
Дәріс № 3
Екі орта арасындағы шекаралық шарттары
Электр және магнит өрістерінің нормаль құрамаларына түсетін шекаралық шарттар.
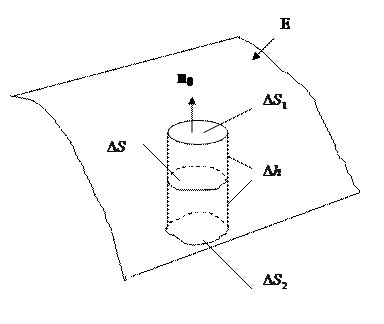
1. сурет
Суретте шекаралық жазықтық көрсетілген. М нүктесі  жазықтығында
жазықтығында
орналасқан. Жазықтықтың жоғарғы жағында бірінші орта  , ал төменгі жағында екінгі орта
, ал төменгі жағында екінгі орта 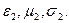
Осы цилиндрға қиғаш ығысу векторының ағыны туседі делік.
Ағын біртекті болсын. Электр күш сызықтары бір біріне параллель болсын,
сонда Е векторын екі векторға ыдыратуға болады. Біріншісі Е1n цилиндрдың
 табанына перпендикуляр, ал екіншісі
табанына перпендикуляр, ал екіншісі  цилиндрдың бүйрек бетіне перпендикуляр. Егер цилиндрды тұйық көлем деп санасақ сонда осы цилиндрды тесіп өтетін ағын сол көлем ішіндегі зарядтардың қосындысына тең болады Остроградский- Гаусс теоремасына сәйкес.
цилиндрдың бүйрек бетіне перпендикуляр. Егер цилиндрды тұйық көлем деп санасақ сонда осы цилиндрды тесіп өтетін ағын сол көлем ішіндегі зарядтардың қосындысына тең болады Остроградский- Гаусс теоремасына сәйкес.

 (1)
(1)
мұнда 
 (2)
(2)
 (3)
(3)
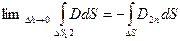 (4)
(4)
Мұндағы минустың пайда болу себебі ағын 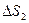 цилиндрдың табанын ішінен сыртқа тесіп өтеді.
цилиндрдың табанын ішінен сыртқа тесіп өтеді.
Сонымен
 (5)
(5)
Цилиндрдың биіктігі азайған сайын көлемі азаяды. Көлем азайса зарядта азаяды, түбінде нольге тең болады.
 (6)
(6)
Немесе
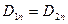 (7)
(7)
Егер екі ортаның шекарасында зарядтар болса онда (5) теңдеу бойынша
 (8)
(8)
Теңдеудің екі жағын  ке бөлсек, сонда оң жағы зарядтардың беттік тығыздығын көрсетеді.
ке бөлсек, сонда оң жағы зарядтардың беттік тығыздығын көрсетеді.
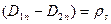 (9)
(9)
Егер зарядтардың беттік тығыздығы нольге тең болса онда
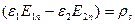 (10)
(10)
 (11)
(11)
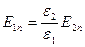 (12)
(12)
Дәл солай біз магнит индукциясын ағынын қарастырып
 (13)
(13)
Көрсетілген әдіспен дәлелдейміз  (14)
(14)
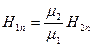 (15)
(15)
Лекция № 4
Электр және магнит өрістерінің жанама құрамаларына түсетін
шекаралық шарттар 
Сурет 2.
Бұл суретте So- екі изотропты орталар арасындағы жазық шекара.
So дан жоғары ортаны сипаттайтын ортаның параметрлары:  .
.
So дан төмен ортаны сипаттайтын ортаның параметрлары: 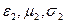 .
.
АВСD – төртбұрыш контур оның жартысы бір ортада, ал екінші жартысы
төменгі ортасында.

no - шекара бетіне М нүктесінен орт векторы, ал  шекара жазықтыққа
шекара жазықтыққа
жанама орт векторы. No - ABCD контурына оң бұранда арқылы табылған орт.
ABCD контурына Максвеллдың бірінші теңдеуін жазайық:
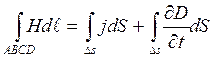 (1)
(1)
Сонда тоқтардың бағыты No векторымен бағыттас болады, ал 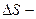 контурдың ауданы.
контурдың ауданы.
 (2)
(2)
BC және DA қабырғалар бір-біріне параллель, ал ұзындықтары 2 қа тең.
қа тең.
AB дағы dl =  , ал CD ның ұзындығы dl =
, ал CD ның ұзындығы dl = 
 (3)
(3)
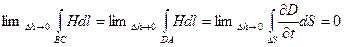 (4)
(4)
 (5)
(5)
Осы шектерді ескере отыра мынандай теңдеуге келеміз:
 (6)
(6)
Егер бөліну шекарасында жазықтық тоқтар жоқ болса онда:
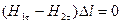 (7)
(7)
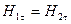 (8)
(8)
Ал 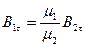 (9)
(9)

Сурет 3
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 910; Нарушение авторских прав?; Мы поможем в написании вашей работы!