Как случайных величин

Характеристика результатов измерений

Количественные измерения

При эмпирических методах исследования в большинстве случаев проводятся измерения. Измерение – это определение значения измеряемой величины путем сравнения ее с эталоном. Конечным результатом измерения являются единичные значения измеряемой величины (первичные данные).

Результаты измерений могут иметь качественный или количественный характер. Качественные значения обычно выражаются словами. Количественные значения – числами.

Пример. Вы измеряли свой рост. Результат измерения можно выразить качественным значением (средний, ниже среднего, выше среднего, низкий, нормальный, высокий и др.). В этом случае за эталон вы приняли рост какого-то человека. Можно представить результат измерения роста и количественным числовым значением, если за эталон вы выбрали какой-нибудь эталон меры (мм, см, м и др.).

Любой результат измерения имеет погрешность в силу влияния на него различных неизвестных или известных, но нерегулируемых факторов. Поэтому результаты измерений относятся к случайным величинам.

Под случайной величиной понимают величину, принимающую значение, которое нельзя точно предсказать (классический пример – числовое значение, появляющееся на верхней грани игрового кубика). Случайная величина имеет набор допустимых значений, но в каждом конкретном случае принимает только одно значение из этого набора. Это значение может быть различным при попытке повторения из-за действия случайных (неизвестных или неконтролируемых) факторов. Набор допустимых значений недостаточен для полной характеристики случайной величины. Необходимо еще указывать вероятность (частоту появления) каждого конкретного значения из этого набора.

Наиболее полной характеристикой любой случайной величины (в том числе и результата измерения) является закон ее распределения. Закон распределения случайной величины – это соотношения между возможными значениями случайной величины и соответствующими им вероятностям. Закон распределения случайной величины может быть представлен графически, в виде таблицы и математической функции (интегральная или дифференциальная функция распределения), из которых можно определить вероятность (Р) появления конкретных значений случайной величины.

Различают дискретные и непрерывные случайные величины. Примером случайной дискретной величины может быть число студентов, присутствующих на лекции (это число, которое может принимать только целочисленное значение, кратное единице). Примером непрерывной случайной величины является масса тела человека, которая может принимать любое значение.

Известно много функций распределения случайных величин. Наиболее часто для непрерывных величин встречаются экспоненциальное и нормальное распределение (распределение Гаусса). На нормальном распределении базируются распределения хи-квадрат (Пирсона), Стьюдента, Фишера и др.

Для дискретных величин может наблюдаться биномиальное распределение, распределение Пуассона и др.

Математические выражения функций распределения имеют достаточно сложный вид. На практике наиболее часто пользуются табличными и графическими формами функций распределения.

Знание закона распределения позволяет также рассчитать некоторые статистические параметры результата измерения как случайной величины используя методы математической статистики. Некоторые параметры и формулы их расчета представлены в табл. 1.

Таблица 1

Параметры результатов измерений и их характеристика

Название	Условное обозначение	Расчетная формула	Краткая характеристика
Единичный результат измерения	y i	-	Результат одного измерения
Выборка единичных результатов измерений	Y n	-	Конечный ряд единичных результатов измерений (y 1, y 2, y 3,..., y i ,..., y n)

Продолжение табл. 1

Название	Условное обозначение	Расчетная формула	Краткая характеристика
Генеральная совокупность результатов измерений	Y	-	Бесконечный ряд единичных результатов измерений (y 1, y 2, y 3,..., y i ,..., y n..., y ¥)
Объем выборки результатов измерений	n	-	Число единичных (повторных) результатов измерений (число членов в ряду Yn)
Среднее арифметическое значение результатов измерений	` y		Один из параметров, наиболее точно оценивающий истинное значение результата измерения
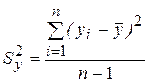
Выборочная дисперсия единичных результатов измерений			Параметр, характеризующий рассеивание (разброс) единичных результатов относительно среднего арифметического результата измерения
Генеральная дисперсия единичных результатов измерения		-	Параметр, характеризующий рассеивание (разброс) единичных результатов относительного истинного результата измерения
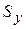
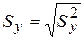
Выборочное среднее квадратическое (абсо­лютное стандартное) отклонение единичного результата измерения			То же (в единицах измерения y i)
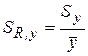
Выборочное относительное стандартное отклонение единичного результата измерения			То же (в долях величины ` y)

Окончание табл. 1

Название	Условное обозначение	Расчетная формула	Краткая характеристика
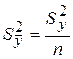
Выборочная дисперсия среднего арифметического результата измерения			Параметр, характеризующий рассеивание (разброс) средних арифметических результатов измерений относительного истинного результата измерения
Выборочное среднее квадратическое (абсо­лютное стандартное) отклонение среднего арифметического результата измерения		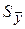	Параметр, характеризующий рассеивание (разброс) средних арифметических результатов измерений относительного истинного результата измерения (в единицах измерения y i)
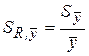
Выборочное относительное стандартное отклонение среднего арифметического результата измерения			То же (в долях величины ` y)
Вероятность получения результата измерения	Р		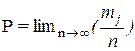При большой величине n величина вероятности Р приближается к частоте получения данного результата измерения y i, т.е. отношению числа y i (mj) в выборке к общему числу измерений
Уровень значимости (ошибки) при получении результата измерения	a	a = 1-Р	При большой величине n величина a приближается к частоте получения результатов измерений, не равных y i

Погрешности измерений

Под погрешностью измерения будем понимать совокупность всех ошибок измерения.

Ошибки измерений можно классифицировать на следующие виды:

- абсолютные и относительные,

- положительные и отрицательные,

- постоянные и пропорциональные,

- грубые,

- случайные и систематические,

- прочие.

Абсолютная ошибка единичного результата измерения (А_y) определяется как разность следующих величин:

А_y = y _i - y _ист.» y _i -` y,

где: y _i – единичный результат измерения; y _ист. – истинный результат измерения; ` y – среднее арифметическое значение результата измерения (далее среднее).

Постоянной называется абсолютная ошибка, которая не зависит от значения измеряемой величины (y» ` y).

Ошибка пропорциональная, если названная зависимость существует. Характер ошибки измерения (постоянная или пропорциональная) определяется после проведения специальных исследований.

Относительная ошибка единичного результата измерения (В_y) рассчитывается как отношение следующих величин:

.

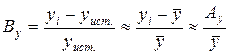Из этой формулы следует, что величина относительной ошибки зависит не только от величины абсолютной ошибки, но и от значения измеряемой величины. При неизменности измеряемой величины (y) относительную ошибку измерения можно уменьшить только за счет снижения величины абсолютной ошибки (А_y). При постоянстве абсолютной ошибки измерения для уменьшения относительной ошибки измерения можно использовать прием увеличения значения измеряемой величины.

Знак ошибки (положительный или отрицательный) определяется разницей между единичным и полученным (средним арифметическим) результатом измерения:

y _i -` y > 0 (ошибка положительная);

y _i -` y < 0 (ошибка отрицательная).

Грубая ошибка измерения (промах) возникает при нарушении методики измерения. Результат измерения, содержащий грубую ошибку, обычно значительно отличается по величине от других результатов. Наличие грубых ошибок измерения в выборке устанавливается только методами математической статистики (при числе повторений измерения n >2). С методами обнаружения грубых ошибок познакомьтесь самостоятельно в [3-6].

К случайным ошибкам относят ошибки, которые не имеют постоянной величины и знака. Такие ошибки возникают под действием следующих факторов: не известных исследователю; известных, но нерегулируемых; постоянно изменяющихся.

Случайные ошибки можно оценить только после проведения измерений.

Количественной оценкой модуля величины случайной ошибки измерения могут являться следующие параметры: выборочная дисперсия единичных значений и среднего значения; выборочные абсолютные стандартные отклонения единичных значений и среднего значения; выборочные относительные стандартные отклонения единичных значений и среднего значения; генеральная дисперсия единичных значений 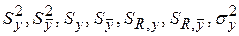), соответственно, и др.

Случайные ошибки измерения невозможно исключить, их можно только уменьшить. Один из основных способов уменьшения величины случайной ошибки измерения – это увеличение числа (объема выборки) единичных измерений (увеличение величины n). Объясняется это тем, что величина случайных ошибок обратно пропорциональна величине n, например:

.

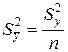Систематические ошибки – это ошибки с неизменными величиной и знаком или изменяющиеся по известному закону. Эти ошибки вызываются постоянными факторами. Систематические ошибки можно количественно оценивать, уменьшать и даже исключать.

Систематические ошибки классифицируют на ошибки I, II и III типов.

К систематическим ошибкам I типа относят ошибки известного происхождения, которые могут быть до проведения измерения оценены путем расчета. Эти ошибки можно исключить, вводя их в результат измерения в виде поправок. Примером ошибки такого типа является ошибка при титрометрическом определении объемной концентрации раствора, если титрант был приготовлен при одной температуре, а измерение концентрации проводилось при другой. Зная зависимость плотности титранта от температуры, можно до проведения измерения рассчитать изменение объемной концентрации титранта, связанное с изменением его температуры, и эту разницу учесть в виде поправки в результате измерения.

Систематические ошибки II типа – это ошибки известного происхождения, которые можно оценить только в ходе эксперимента или в результате проведения специальных исследований. К этому типу ошибок относят инструментальные (приборные), реактивные, эталонные и др. ошибки. Познакомьтесь с особенностями таких ошибок самостоятельно в [5].

Любой прибор при его применении в процедуре измерения вносит в результат измерения свои приборные ошибки. При этом часть этих ошибок случайная, а другая часть – систематическая. Случайные ошибки приборов отдельно не оценивают, их оценивают в общей совокупности со всеми другими случайными ошибками измерения.

Каждый экземпляр любого прибора имеет свою персональную систематическую ошибку. Для того чтобы оценить эту ошибку, необходимо проводить специальные исследования.

Наиболее надежный способ оценки приборной систематической ошибки II типа – это сверка работы приборов по эталонам. Для мерной посуды (пипетка, бюретка, цилиндры и др.) проводят специальную процедуру – калибровку.

На практике наиболее часто требуется не оценить, а уменьшить или исключить систематическую ошибку II типа. Самыми распространенными методами уменьшения систематических ошибок являются методы релятивизации и рандомизации. Познакомьтесь с этими методами самостоятельно в [5].

К ошибкам III типа относят ошибки неизвестного происхождения. Эти ошибки можно обнаружить только после устранения всех систематических ошибок I и II типов.

К прочим ошибкам отнесем все другие виды ошибок, не рассмотренные выше (допускаемые, возможные предельные ошибки и др.).

Понятие возможных предельных ошибок применяется в случаях использования средств измерения и предполагает максимально возможную по величине инструментальную ошибку измерения (реальное же значение ошибки может быть меньше величины возможной предельной ошибки).

При использовании средств измерения можно рассчитать возможную предельную абсолютную (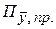) или относительную () погрешность измерения. Так, например, возможная предельная абсолютная погрешность измерения находится как сумма возможных предельных случайных () и неисключенных систематических () ошибок:

= +

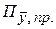При выборках малого объема (n £ 20) неизвестной генеральной совокупности, подчиняющейся нормальному закону распределения, случайные возможные предельные ошибки измерений можно оценить следующим образом:

= = ,

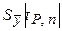где: – доверительный интервал для соответствующей вероятности Р;

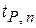– квантиль распределения Стьюдента для вероятности Р и выборки объемом n или при числе степеней свободы f = n – 1.

Абсолютная возможная предельная погрешность измерения в этом случае будет равна:

= + .

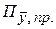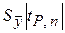Если результаты измерений не подчиняются нормальному закону распределения, то оценка погрешностей проводится по другим формулам.

Определение величины зависит от наличия у средства измерения класса точности. Если средство измерения не имеет класса точности, то за величину можно принять минимальную цену деления шкалы (или ее половину) средства измерения [5]. Для средства измерения с известным классом точности за величину можно принять абсолютную допускаемую систематическую ошибку средства измерения ():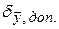

».

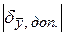Величина 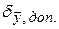рассчитывается исходя из формул, приведенных в табл. 2.

Для многих средств измерения класс точности указывается в виде чисел а ×10 ⁿ, где а равно 1; 1,5; 2; 2,5; 4; 5; 6 и n равно 1; 0; -1; -2 и т.д., которые показывают величину возможной предельной допускаемой систематической ошибки (Е _{y , доп.} ) и специальных знаков, свидетельствующих о ее типе (относительная, приведенная, постоянная, пропорциональная).

Если известны составляющие абсолютной систематической ошибки среднего арифметического результата измерения (например, приборная ошибка, ошибка метода и др.), то ее можно оценить по формуле

,

где: m – число составляющих систематическую ошибку среднего результата измерения;

k – коэффициент, определяемый вероятностью Р и числом m;

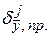– абсолютная систематическая ошибка отдельной составляющей.

Отдельными составляющими погрешности можно пренебрегать при выполнении соответствующих условий.

Таблица 2

Примеры обозначения классов точности средств измерения

Обозначение класса точности	Формула расчета и значение предельной допускаемой систематической ошибки	Характеристика систематической ошибки
в документации	на средстве измерения
1,5	1,5		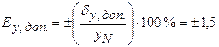Приведенная допускаемая систематическая ошибка в процентах от номинального значения измеряемой величины, которое определяется типом шкалы средства измерения
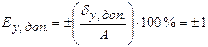
1			Приведенная допускаемая систематическая ошибка в процентах от длины использованной шкалы средства измерения (А) при получении единичных значений измеряемой величины
0,5	0,5		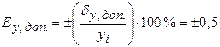Постоянная относительная допускаемая систематическая ошибка в процентах от полученного единичного значения измеряемой величины
0,02/ 0,01	0,02/ 0,01	c = 0,02; d = 0,01	Пропорциональная относительная допускаемая систематическая ошибка в долях от полученного единичного значения измеряемой величины, которая возрастает при увеличении конечного значения диапазона измерения данным средством измерения (y k) или уменьшении единичного значения измеряемой величины (y i)

Систематическими ошибками можно пренебрегать, если выполняется неравенство

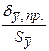< 0,8.

В этом случае принимают

» » » .

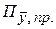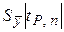Случайными ошибками можно пренебречь при условии

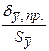> 8.

Для этого случая » .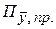

Чтобы общая погрешность измерения определялась только систематическими ошибками, увеличивают число повторных измерений. Минимально необходимое для этого число повторных измерений (n _min) можно рассчитать только при известном значении генеральной совокупности единичных результатов по формуле

.

Оценка погрешностей измерения зависит не только от условий измерения, но и от типа измерения (прямое или косвенное).

Деление измерений на прямые и косвенные достаточно условно. В дальнейшем под прямыми измерениями будем понимать измерения значения которых берут непосредственно из опытных данных, например, считывают со шкалы прибора (широко известный пример прямого измерения – измерение температуры термометром). К косвенным измерениям будем относить такие, результат которых получают на основании известной зависимости между искомой величиной и величинами, определяемыми в результате прямых измерений. При этом результат косвенного измерения получают расчетным путем как значение функции j, аргументами которой являются результаты прямых измерений (x ₁, x ₂, …, x _j,.…, x _k).

Необходимо знать, что ошибки косвенных измерений всегда больше, чем ошибки отдельных прямых измерений.

Ошибки косвенных измерений оцениваются по соответствующим законам накопления ошибок (при k ³ 2).

Закон накопления случайных ошибок косвенных измерений выглядит следующим образом:

.

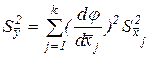Закон накопления возможных предельных абсолютных систематических ошибок косвенных измерений представляется следующими зависимостями:

; .

Закон накопления возможных предельных относительных систематических ошибок косвенных измерений имеет следующий вид:

;

.

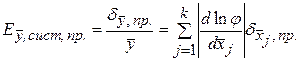В случаях, когда искомая величина (y) рассчитывается как функция результатов нескольких независимых прямых измерений вида , закон накопления предельных относительных систематических ошибок косвенных измерений принимает более простой вид:

; .

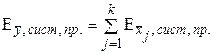Ошибки и погрешности измерений определяют их точность, воспроизводимость и правильность.

Точность тем выше, чем меньше величина погрешности измерения.

Воспроизводимость результатов измерений улучшается при уменьшении случайных ошибок измерений.

Правильность результата измерений увеличивается с уменьшением остаточных систематических ошибок измерений.

Более подробно с теорией ошибок измерений и их особенностями познакомьтесь самостоятельно [4,5]. Обращаю ваше внимание на то, что современные формы представления конечных результатов измерений обязательно требуют приведения ошибок или погрешностей измерения (вторичных данных). При этом погрешности и ошибки измерений должны представляться числами, которые содержат не более двух значащих цифр [3].

Дата добавления: 2014-01-07