
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формы представления конечных результатов измерений
|
|
|
|
Для представления количественных результатов измерений (при неизвестных параметрах генеральной совокупности) можно использовать следующие формы:
форма 1 – при одном единичном значении результата измерений
(n = 1):
y = y 1 ±  ;.
;.
форма 2 – при наличии нескольких единичных результатов измерений (n ³ 2) и отсутствии сведений о функции их распределения:
y = ` y; 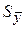 ; n;
; n;  ;
;
форма 3 – при наличии нескольких единичных результатов измерений (n ³ 2) и знании функции их распределения:
а) y =` y ±  ; P (при симметричной погрешности);
; P (при симметричной погрешности);
б) y =` y;  от
от  до
до 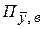 ; P (для несимметричной погрешности, где
; P (для несимметричной погрешности, где  – общая абсолютная погрешность;
– общая абсолютная погрешность;  – нижняя граница общей абсолютной погрешности, а
– нижняя граница общей абсолютной погрешности, а 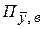 – верхняя граница общей абсолютной погрешности).
– верхняя граница общей абсолютной погрешности).
При окончательном представлении фактического результата измерения число значащих цифр и разрядов после десятичной запятой должно быть скорректировано исходя из точности математических вычислений и погрешности измерения.
Приведу пример статистической обработки первичных данных измерения с целью получения и представления конечного результата измерения.
 Пример. При трехкратном взвешивании образца на аналитических весах (класс точности 0,01 ) были считаны с табло весов следующие единичные результаты измерения массы образца (неисправленные результаты единичных измерений, m¢i): 1,2356; 1,2345; 1,2348 г. Результаты метрологической поверки весов свидетельствуют об их отрицательной постоянной абсолютной систематической ошибке lm, равной минус 0,0003 г.
Пример. При трехкратном взвешивании образца на аналитических весах (класс точности 0,01 ) были считаны с табло весов следующие единичные результаты измерения массы образца (неисправленные результаты единичных измерений, m¢i): 1,2356; 1,2345; 1,2348 г. Результаты метрологической поверки весов свидетельствуют об их отрицательной постоянной абсолютной систематической ошибке lm, равной минус 0,0003 г.
Значения исправленных единичных результатов измерений (mi) рассчитаем по формуле

Тогда ряд исправленных единичных результатов измерения массы образца будет иметь вид: 1,2359; 1,2348; 1,2351 г.
Первоначально проведем поиск грубых ошибок измерения (промахов). Так как для данной выборки n равен 3 (n < 8 ), то согласно [ 3 ] для обнаружения промахов используем Q-критерий. Единичные результаты измерений представим в виде нового ряда с возрастающими величинами массы образца: 1,2348; 1,2351; 1,2359 г. Проверим на промахи крайние члены этого нового ряда, которые кажутся сомнительными:
Для крайних членов ряда, m1 и m3, определим соответствующие им расчетные значения Q1 и Q3 по формуле

где 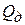 –расчетные значения, mn – проверяемый результат, mn-1 – результат соседний в ряду с проверяемым, R – размах выборки, равный модулю разности крайних членов числового ряда.
–расчетные значения, mn – проверяемый результат, mn-1 – результат соседний в ряду с проверяемым, R – размах выборки, равный модулю разности крайних членов числового ряда.
Вычисленные значения Q1 и Q3 будут равны:
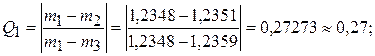

В литературных данных находим табличное значение Q-критерия (QТ = = 0,94) для объема выборки n = 3 и вероятности Р = 0,95 (принимаем наиболее часто задаваемое значение вероятности в химии и химической технологии) по следующим табличным данным [3]:
| Объем выборки п | Значения критерия Q для доверительной вероятности Р | ||
| 0,90 | 0,95 | 0,99 | |
| 0,89 | 0,94 | 0,99 | |
| 0,68 | 0,77 | 0,89 | |
| 0,56 | 0,64 | 0,76 | |
| 0,48 | 0,56 | 0,70 | |
| 0,43 | 0,51 | 0,64 | |
| 0,40 | 0,48 | 0,68 |
Так как в обоих случаях QТ (0,94) > QР, то проверяемые результаты не являются грубыми ошибками измерения, поэтому оставляем их в выборке для дальнейшей статистической обработки.
Учитывая, что для непредставительных выборок (n < 10) не рекомендуется проверять их подчинение законам распределения, сделаем допущение о соответствии единичных результатов измерения массы образца нормальному закону распределения. Так как истинный закон распределения результатов измерений неизвестен, то для представления конечных результатов измерения выберем форму 2.
Выполним следующие расчеты с учетом точности математических вычислений со случайными числами [3] и правил округления.
Определим среднее арифметическое значение массы образца (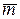 ):
):
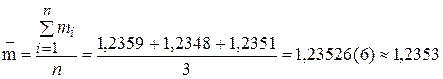 г.
г.
Рассчитаем выборочное абсолютное стандартное отклонение среднего арифметического значения 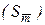 , оценивающее случайную ошибку измерения:
, оценивающее случайную ошибку измерения:
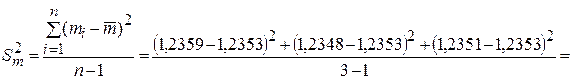
 (г)2;
(г)2;
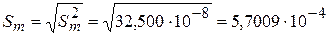 г;
г;
 × 10-4 г .
× 10-4 г .
Делаем допущение, что систематические ошибки весов превосходят прочие систематические ошибки, которыми можно пренебречь. По классу точности весов рассчитаем возможные предельные относительную ( ) и абсолютную (
) и абсолютную ( ) систематические ошибки измерений по допускаемым систематическим ошибкам прибора.
) систематические ошибки измерений по допускаемым систематическим ошибкам прибора.
Исходя из величины (0,01) и обозначения (замкнутый контур) класса точности весов, допускаемая относительная систематическая ошибка весов равна 0,01%, а формула для расчета допускаемой абсолютной систематической ошибки среднего арифметического значения будет выглядеть следующим образом:
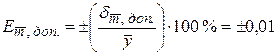 %.
%.
Тогда возможные предельные систематические ошибки среднего арифметического значения будут равны:
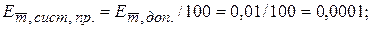
 г.
г.
Рассчитаем возможную предельную общую погрешность среднего арифметического значения ( ) по формуле
) по формуле
 =
=  +
+ 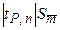 ,
,
где 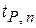 – квантиль распределения Стьюдента для вероятности Р при объеме выборки n.
– квантиль распределения Стьюдента для вероятности Р при объеме выборки n.
В табл. А.2 приложения А для вероятности Р = 0,95 при объеме выборки n = 3 (число степеней свободы f = n –1 =2 ) находим квантиль распределения Стьюдента: = 4,3.
= 4,3.
Тогда:
 = 1,2353·10-4 +4,3×3,2914×10-4= 1,538832×10-3» 2×10-3 г(так как в погрешности оставляем только первую значащую цифру с учетом округления).
= 1,2353·10-4 +4,3×3,2914×10-4= 1,538832×10-3» 2×10-3 г(так как в погрешности оставляем только первую значащую цифру с учетом округления).
Средний арифметический результат измерения скорректируем по первой значащей цифре возможной предельной общей погрешности измерения, то есть до третьего знака после запятой:
`m = 1,2353 ≈ 1,235 г.
Таким образом, по форме 2 при применении принципа приведения одной первой значащей цифры в погрешности и ошибках измерения, окончательный результат измерения массы образца будет выглядеть следующим образом:
m = 1,235 г;  = 3×10-4 г ; n = 3;
= 3×10-4 г ; n = 3; 
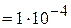 г.
г.
При применении принципа приведения двух первых значащих цифр в погрешности и ошибках измерения окончательный результат измерения массы образца будет следующим:
m = 1,2353 г;  = 3,3×10-4 г; n = 3;
= 3,3×10-4 г; n = 3; 
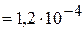 г.
г.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 332; Нарушение авторских прав?; Мы поможем в написании вашей работы!