Анализ поля корреляции

Проведения корреляционного анализа

Корреляционный анализ не накладывает повышенных требований к планированию эксперимента. Единственным обязательным условием является выполнение соотношения m_j > 2.

Из рекомендаций по планированию эксперимента для проведения корреляционного анализа можно привести следующие. Желательно, чтобы план эксперимента предусматривал:

- широкую область изменения значений факторов x _j;

- большое число m_j значений (уровней) факторов x _j, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения;

- повторные опыты для каждого значения (уровня) факторов x _j;

- большое общее число измерений (N).

Пример. При проведении 4 опытов эксперимента по исследованию влияния времени реакции (х) на выход пентозанов (y) при гидролизе березовых опилок был получен ряд единичных результатов измерений (табл. 6).

Таблица 6

Результаты эксперимента

Параметры эксперимента	Значения параметров в опытах
№ 1	№ 2	№ 3	№ 4
x, мин.	100	110	120	130
y, отн. %	20	40	50	60

Корреляционный анализ полученных результатов измерений проведем двумя методами: анализируя поле корреляции и выборочный коэффициент парной линейной корреляции.

При использовании этого метода выполняем две операции:

- строим поле корреляции (см. рис. 4);

- проводим анализ построенного поля корреляции.

Анализ поля корреляции (рис. 4) позволяет сделать предварительные выводы.

1. Есть зависимость выхода пентозанов от времени гидролиза, т.е. время реакции оказывает влияние на выход пентозанов.

2. Данная зависимость является корреляционной параболической.

3. Знак зависимости положительный.

4. Зависимость является тесной.

Анализ выборочного коэффициента парной линейной корреляции.

Выполняем следующие операции:

1) рассчитываем выборочный парный коэффициент линейной корреляции r_yx;

2) проверяем нуль-гипотезу для рассчитанного значения r_yx;

3) анализируем окончательное значение r_yx.

Для выполнения расчета r_yx первоначально рассчитываем следующие величины:

мин.

отн. %;

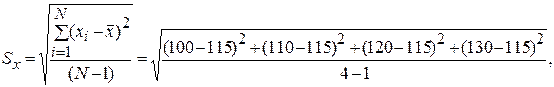
S_x = 12,9 мин (в результате расчета оставлены три значащие цифры в соответствии с точностью математических вычислений (см. [3]);

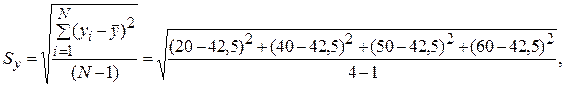
S_y = 17,078 » 17 отн. %.

Тогда значение r_yx будет равно:

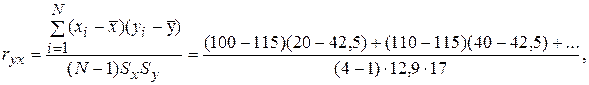
r_yx = 0,983» 0,98.

Для проверки нуль-гипотезы рассчитанного значения r_yx воспользуемся методом, описанным в [3]. Согласно этому методу рассчитаем значение квантиля распределения Стьюдента (t_р) по формуле:

.

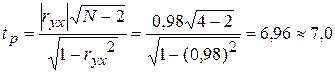Табличное значение квантиля распределения Стьюдента (t_т), если примем вероятность Р = 0,95 и вычислим число степеней свободы f (f =N–– 2 = 4–2 = 2 ), будет равно 4,3 (прил. А). Сравним t_т и t_р: t _т < t_р ( 4,30 < 7,0 ).

Из этого неравенства следует, что с вероятностью Р = 0,95 нуль-гипотеза не выполняется, т.е. необходимо считать, что r_yx ¹ 0, т.е.
r_yx = 0,98.

Анализ выборочного коэффициента парной линейной корреляции позволяет сделать предварительные выводы.

1. Есть линейная зависимость выхода пентозанов от времени гидролиза с вероятностью 0,95, т.е. время реакции оказывает влияние на выход пентозанов при гидролизе березовых опилок.

2. Данная зависимость является корреляционной.

3. Знак зависимости – положительный.

4. Зависимость является очень тесной.

Если же задать более высокую вероятность, например Р= 0,99, то тогда t_т = 9,93 и из неравенства t_т > t_р следует, что с вероятностью Р = = 0,99 выполняется нуль-гипотеза, т.е. необходимо считать, что r_yx = 0. Значит, для вероятности 0,99 выводы корреляционного анализа будут другими, по сравнению с вероятностью 0,95.

Окончательные выводы корреляционного анализа.

Совместный анализ поля корреляции и окончательного значения выборочного коэффициента парной линейной корреляции (r_yx = 0,98) позволяет сделать выводы.

1. Есть зависимость выхода пентозанов от времени гидролиза (в изученном диапазоне времени), т.е. время реакции оказывает влияние на выход пентозанов при гидролизе березовых опилок.

2. Данная зависимость с вероятностью 0,95 является корреляционной линейной.

3. Знак зависимости положительный.

4. Зависимость является очень тесной.

Контрольные вопросы и задания

1. Для каких целей применяют корреляционный анализ в научных исследованиях?

2. Приведите названия предельных случаев корреляционной связи между свойством объекта Y и фактором X.

3. Укажите единственное обязательное условие при планировании эксперимента для последующей обработки его результатов методами корреляционного анализа.

4. Какой метод корреляционного анализа является наиболее точным и почему?

Дата добавления: 2014-01-07