Общие положения дисперсионного анализа

Дисперсионного анализа

Планирование эксперимента для применения

Дисперсионный анализ – это метод математической статистики, который также как и корреляционный анализ позволяет качественно устанавливать связь между случайными величинами.

Суть дисперсионного анализа заключается в сравнении между собой двух или более дисперсий и доказательстве нуль-гипотезы разности этих дисперсий.

При установлении зависимости j дисперсионным анализом исходят из следующих соображений.

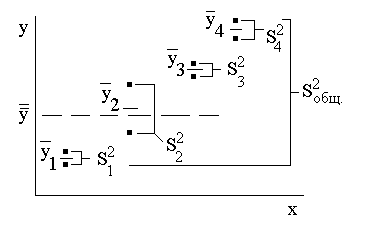
В эксперименте изменения средних арифметических значений свойства объекта (` y<sub>v</sub>) зависят не только от изменяемых факторов x <sub>j</sub> (с известными уровнями), но и от случайных факторов. Поэтому рассеивание (разброс)` y _v относительно общего среднего арифметического значения 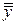(рис. 5), характеризуемое общей дисперсией (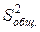), разделяется на составляющие: рассеивание, обусловленное случайными факторами (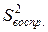), и рассеивание, обусловленное известными факторами за счет изменения их значений, т.е. перехода с одного уровня на другие ().

Рис. 5. Поле корреляции величин y и x

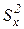Попарное сравнение факторной дисперсии (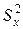) с дисперсией, характеризующей действие случайных факторов, т.е. воспроизводимость эксперимента (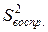), позволяет на основании закона распределения Фишера сделать следующие основные выводы дисперсионного анализа:

1) установить или опровергнуть влияние x _j на y с заданной вероятностью ("влияет", "не влияет" и др.);

2) определить вероятность влияния x _j на y.

Так, например, после проведения эксперимента и математической обработки результатов измерений можно вычислить F-отношение (F_p):

; ; .

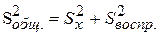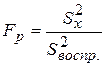Задав вероятность Р и вычислив по известным формулам числа степеней свободы для факторной дисперсии f_факт. (f₁) и дисперсии воспроизводимости f_воспр. (f₂), из справочных данных выбираем табличное значение квантиля распределения Фишера (F _т). При выполнении неравенства F_P > > F _т можно делать вывод, что данный фактор х с вероятностью Р влияет на свойство y, т.е. "значима" разность между влиянием на свойство y известного фактора х и случайных факторов. При невыполнении этого неравенства делается вывод об отсутствии влияния фактора х на свойство y, т.е. это влияние соизмеримо со случайными ошибками эксперимента.

Дисперсионный анализ по сравнению с корреляционным анализом имеет существенные преимущества.

1) позволяет делать однозначные и более точные выводы о влиянии фактора x _j на свойство y;

2) позволяет определить влияние на свойство y не только количественных, но и качественных факторов (например, типа растворителя, времени года и др.);

3) позволяет оценить значение (уровень) фактора x _j, при котором он начинает влиять с заданной вероятностью на свойство y.

Методы проведения дисперсионного анализа зависят от числа известных факторов, одновременно изменяемых в эксперименте. Различают планы экспериментов для проведения одно-, двух- и многофакторного (трех- и более) дисперсионного анализа.

Дата добавления: 2014-01-07