Метод симплекс-планирования

Название метода произошло от названия геометрической фигуры "регулярный симплекс", т.е. правильный выпуклый многогранник. Если исследуется влияние на свойство объекта k факторов, то факторное пространство можно задать в виде регулярного симплекса с (k + 1) вершиной. Так, например, для двух факторов (k = 2) факторное пространство можно задать в виде правильного треугольника (правильный многогранник с 3 вершинами), а для трех факторов (k = 3) – в виде тетраэдра (правильный многогранник с 4 вершинами).

Разработаны [4, 13] простые в построении матрицы планов эксперимента с использованием для исследований факторного пространства регулярных симплексов. Центр регулярных симплексов совпадает с центром факторного пространства (координаты центра начального плана эксперимента задаются в кодированных значениях как х_j = 0). Одна из вершин исходного симплекса лежит на одной из координатных осей этого пространства. Для такого случая построение плана эксперимента начинается с матрицы Е с кодированными значениями факторов (табл. 19).

Данные табл. 19 показывают, что число опытов в исходном симплекс-плане (N) всегда на единицу больше числа исследуемых факторов k (N = k + 1).

Конкретные цифровые значения х_j рассчитываются по формуле

x_j = .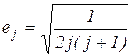

После завершения эксперимента по исходному симплекс-плану оценивают полученные значения отклика объекта и определяют номер опыта (h) с наихудшим для исследователя значением y (минимальным или максимальным в зависимости от цели оптимизации). По координатам наихудшего опыта рассчитывают координаты нового дополнительного (k + 2) опыта:

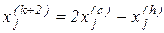; при i ¹ h.

После реализации нового опыта (k + 2) вновь анализируют значения y и если значение y^k+2 лучше значения y^h, снова определяют номер наихудшего опыта во всей совокупности проведенных опытов (исключая из рассмотрения опыт h) и рассчитывают координаты следующего дополнительного (k +3) опыта. Если новый опыт не приводит к получению лучшего значения y, то эксперименты заканчивают и за рациональное значение факторов принимают координаты опыта, в котором получено наилучшее значение y.

Таблица 19

Исходный симплекс-план эксперимента

с кодированными значениями факторов

Номер	Кодированные значения факторов	y
опыта i	х1	х2	х3	…	хj	…	xk-1	xk
	e 1	e 2	e 3	…	e j	…	e k-1	e k
	- 1 e 1	e 2	e 3	…	e j	…	e k-1	e k
		-2 e 2	e 3	…	e j	…	e k-1	e k
			-3 e 3	…	e j	…	e k-1	e k
…				…	e j	…	e k-1	e k
j+1					-j e j	…	e k-1	e k
…						…	e k-1	e k
k							-(k-1) e k-1	e k
k+1								-k e k

Достоинства метода симплекс-планирования:

- экономное число опытов из-за необязательности их повторения;

- возможность увеличения числа исследуемых факторов на любом этапе исследований без значительного увеличения числа опытов;

- возможность при оптимизации одного свойства объекта учитывать изменения других свойств;

- возможность получения уравнения регрессии по симплекс-планам при k = 4 a –1, где а равно 1,2,3, … n.

Недостатки метода симплекс-планирования:

- позволяет найти только один экстремум функции отклика объекта, а для поиска других экстремумов необходимо повторять реализацию исходного симплекс-плана в другой области факторного пространства;

- эффективность поиска экстремумов функции отклика объекта зависит от величины выбранного интервала варьирования факторов.

Для поиска всех возможных экстремумов функции отклика объекта проводят исследование ее поверхности по уравнению регрессии в стандартном каноническом виде [4]. Методы решения оптимизационных задач реализованы в различных программных продуктах, например в Excel [14, 15].

Контрольные вопросы

1. Какой из методов решения оптимизационных задач не требует знания уравнения регрессии?

2. Что необходимо предпринять, если есть опасение, что найден локальный экстремум функции отклика объекта?

Дата добавления: 2014-01-07