Метод крутого восхождения или наискорейшего спуска по поверхности функции отклика объекта

Оптимизационных задач

Планирование эксперимента для решения

Оптимизационные задачи в большинстве случаев формулируются как задачи поиска экстремальных значений функции отклика объекта (максимумов или минимумов). Например, инженеру часто приходится решать задачи поиска оптимальных условий производства продукции с максимальной производительностью и минимальной себестоимостью.

Поведение объекта во многих случаях приходится описывать несколькими функциями отклика. Очень редко удается найти такое сочетание значений всех влияющих факторов, при которых достигаются все желаемые экстремумы функций отклика объекта. Большинство влияющих факторов можно изменять только в реальных пределах: концентрации реагентов не могут быть отрицательными, температуры процессов не могут превышать безопасные значения и т.д. Исследователю нужны и реальные значения функции отклика объекта: неотрицательные значения выхода продукции, степени очистки, себестоимости продукции и др. Поэтому в большинстве случаев оптимизационные задачи решают при условии различных ограничений величины влияющих факторов и значений функций откликов объектов, т.е. проводят поиск рациональных значений влияющих факторов.

При традиционном поиске рациональных условий стабилизируют все факторы, кроме одного. При этом зачастую обнаруживается только часть экстремальных значений функции отклика объекта (²локальные² экстремумы).

Для получения более полной информации о поведении объекта рекомендуется проводить поиск рациональных условий при одновременном изменении нескольких факторов, используя специальные методы математического планирования эксперимента [4].

Все методы математического планирования эксперимента для решения оптимизационных задач делят на две группы: методы, требующие знаний уравнения регрессии функции отклика объекта, и методы, не требующие таких знаний.

К группе методов, требующих знаний уравнения регрессии функции отклика объекта, относятся:

- метод крутого восхождения или наискорейшего спуска по поверхности функции отклика объекта;

- метод обобщенной функции желательности;

- другие методы. К ним относится симплекс-метод, или метод симплекс-планирования эксперимента.

Коротко рассмотрим суть некоторых из этих методов.

Применение данного метода начинается с получения функции отклика объекта в виде исходного уравнения регрессии [4]. Для этого выбирают влияющие факторы и области их изменения (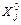, D X_j), планируют и реализуют план эксперимента первого или второго порядка.

После нахождения исходного уравнения регрессии определяют шаг и направление поиска экстремума функции отклика объекта. Для этого один из факторов принимают за базовый и для него выбирают шаг движения, который должен быть не больше шага варьирования этого фактора при получении исходного уравнения регрессии (D Х_j), например, если за базовый фактор взять Х ₁, то для базового шага движения (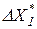) должно выполняться соотношение .

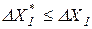Шаги движения остальных факторов рассчитывают следующим образом:

; ,

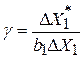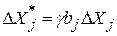где b_j – линейные эффекты факторов (с учетом их знаков!) в исходном уравнении регрессии.

Движение к экстремуму функции отклика объекта начинают из центра плана эксперимента, использованного при получении исходного уравнения регрессии (X_j = 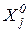, x_j = 0).

При поиске максимума функции отклика объекта (метод крутого восхождения) для определения условий проведения последующего опыта к координатам предыдущего опыта в факторном пространстве прибавляют шаги движения по каждому фактору. При поиске минимума (метод наискорейшего спуска) из координат предыдущего опыта вычитают шаги движения.

Движение к экстремуму прекращают в следующих случаях:

- значения функции отклика объекта или хотя бы одного фактора вышли за пределы допустимых значений;

- найден экстремум (возможно, локальный) функции отклика объекта.

В первом случае оптимизацию заканчивают. Во втором случае проводят дополнительные эксперименты по получению нового уравнения регрессии в области обнаруженного экстремума и поиску нового экстремума на основе нового уравнения регрессии.

К недостаткам метода крутого восхождения или наискорейшего спуска следует отнести довольно большое число экспериментов при его реализации.

С конкретными примерами применения метода крутого восхождения или наискорейшего спуска можно познакомиться в литературе [4, 13].

Дата добавления: 2014-01-07