H1 s1 s1

F1

H2 f2

B1 B1

K1 C1

A1 aD1 C1 A1

D1 D 1

A2 A2

B2 B2

K2

a1 a1

Рис. 5 Определение точки пересечения прямой с плоскостью

Решение задачи сводится к нахождению точки (К2) встречи прямой с плоскостью на фронтальной плоскости проекций. Видимость определяется по общему алгоритму.

Построение перпендикуляра к плоскости

В практике часто требуется восстановить перпендикуляр к плоскости из какой-либо точки или найти кратчайшее расстояние от точки до плоскости, т.е. опустить перпендикуляр на плоскость из заданной точки.

В курсе элементарной геометрии доказывается, что для того, чтобы прямая была перпендикулярна плоскости, достаточно чтобы она была перпендикулярна любым двум прямым, лежащим в данной плоскости (рис.6).

Таким образом, для построения перпендикуляра с плоскости в ней необходимо выбрать две любые пересекающиеся прямые и построить прямую (а), составляющую с каждой из них прямой угол.

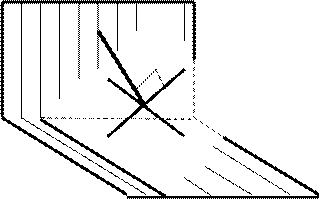
В качестве таких прямых следует

принимать линии уровня (f, h), так

а как в этом случае может быть

· f использована теорема о проекции

h прямого угла на плоскость.

Q На эпюре эта теорема

представлена рис. 6.

Рис. 6 Перпендикуляр к плоскости

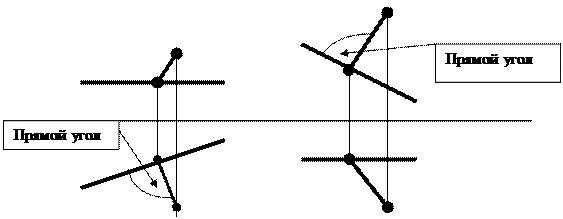
Важно отметить, что горизонтальная проекция прямой, перпендикулярной плоскости всегда перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция перпендикулярна фронтальной проекции фронтали (рис.7).

S2 S2

Рис.7 Эпюр перпендикуляра к прямым уровня

Задачи на перпендикулярность решаются по общему алгоритму:

1. В плоскости провести горизонталь и фронталь.

2. К горизонтальной проекции горизонтали либо восстановить перпендикуляр, либо опустить перпендикуляр (по условию задачи).

3. Достроить недостающие проекции перпендикуляра.

4. Найти натуральную величину перпендикуляра.

5. Определить видимость изображения.

Воспользуемся данным алгоритмом и решим задачу по этапам.

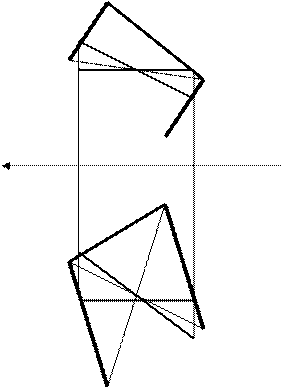
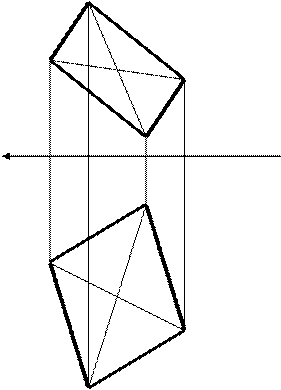
Пример 3. Построить четырехгранную пирамиду с основанием АВСD и высотой 50 мм, восстановленной из точки О (рис. 8).

Рассмотрим алгоритм решения задачи:

1. В плоскости АВСD построим фронталь - f [2111] и найдем ее фронтальную проекцию (2212), рис 8, а.

2. В плоскости АВСD построим горизонталь - h [3242] и найдем ее горизонтальную проекцию (3141) рис. 8,а.

Дано: Решение (1 этап):

В2 В2

22

А2 А 2 f2 42

Дата добавления: 2014-01-07